Cho hình ABCD (AB // DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC

Bài 4.5 trang 48 SBT Toán 8 Tập 1: Cho hình ABCD (AB // DC). Một đường thẳng song song với hai đáy cắt các đoạn thẳng AD, AC, BC theo thứ tự tại M, I, N. Chứng minh rằng:

a) $\frac{AM}{MD}=\frac{BN}{NC};$

b) $\frac{AM}{AD}+\frac{CN}{CB}=1.$

Trả lời

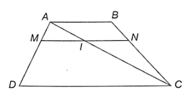
a) Xét tam giác ADC, MI // DC nên theo định lí Thalès ta có: $\frac{AM}{MD}=\frac{AI}{IC}$.

Xét tam giác ABC, IN // AB nên theo định lí Thalès ta có: $\frac{AI}{IC}=\frac{BN}{NC}$.

Từ đó, suy ra $\frac{AM}{MD}=\frac{BN}{NC}$.

b) Xét tam giác ADC, MI // DC nên theo định lí Thalès ta có: $\frac{AM}{AD}=\frac{AI}{AC}$.

Xét tam giác ABC, IN // AB nên theo định lí Thalès ta có: $\frac{CN}{CB}=\frac{CI}{CA}$.

Khi đó $\frac{AM}{AD}+\frac{CN}{CB}=\frac{AI}{AC}+\frac{CI}{CA}=\frac{AI+CI}{CA}=\frac{AC}{CA}=1$.

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài 14: Hình thoi và hình vuông

Bài tập cuối chương 3

Bài 15: Định lí Thalès trong tam giác

Bài 16: Đường trung bình của tam giác

Bài 17: Tính chất đường phân giác của tam giác

Bài tập cuối chương 4