Bài 4.6 trang 48 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có M, N lần lượt là trung điểm của AB và CD. Gọi P, Q theo thứ tự là giao điểm của AN và CM với đường chéo BD. Chứng minh rằng: DP = PQ = QB.
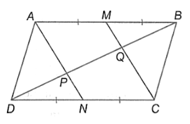
Do ABCD là hình bình hành nên AB // CD, AB = CD
Mà M, N lần lượt là trung điểm của AB và CD nên AM // NC và AM = NC
Tứ giác AMCN có AM // NC và AM = NC nên AMCN là hình bình hành.
Suy ra AN // MC.
Xét tam giác ABP, MQ // AP nên theo định lí Thalès ta có:
Do đó BQ = QP. (1)
Xét tam giác DQC, PN // QC nên theo định lí Thalès ta có:
Do đó DP = PQ. (2)
Từ (1) và (2) suy ra BQ = QP = PD.
Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:
Bài 14: Hình thoi và hình vuông
Bài 15: Định lí Thalès trong tam giác
Bài 16: Đường trung bình của tam giác