Giải SBT Toán 7 (Chân trời sáng tạo) Bài 2: Đại lượng tỉ lệ thuận

Giải Sách bài tập Toán lớp 7 Bài 2: Đại lượng tỉ lệ thuận

Giải SBT Toán 7 trang 11 Tập 2

Bài 1 trang 11 SBT Toán 7 Tập 2: Cho hai đại lượng x và y tỉ lệ thuận với nhau. Biết rằng khi x = 3 thì y = 9.

a) Tìm hệ số tỉ lệ của x đối với y.

b) Tính giá trị của y khi x = –7.

Lời giải:

a) Gọi hệ số tỉ lệ của x đối với y là k (k ≠ 0).

Do x và y tỉ lệ thuận với nhau nên suy ra $k=\frac{x}{y}.$

Khi x = 3 và y = 9 ta có $k=\frac{3}{9}=\frac{1}{3}.$

Vậy hệ số tỉ lệ của x đối với y là  $\frac{1}{3}$ .

b) Theo câu a ta có công thức $x=\frac{1}{3}y$  suy ra y = 3x.

Khi  x = -7, ta có y = 3 . (-7) = -21.

Vậy y = -21.

Bài 2 trang 11 SBT Toán 7 Tập 2: Cho hai đại lượng a và b tỉ lệ thuận với nhau. Biết rằng khi a = 5 thì b = –10.

a) Tìm hệ số tỉ lệ của b đối với a và biểu diễn b theo a.

b) Tìm hệ số tỉ lệ của a đối với b và biểu diễn a theo b.

Lời giải:

a) Gọi hệ số tỉ lệ của b đối với a là k (k ≠ 0).

Do hai đại lượng a và b tỉ lệ thuận với nhau nên ta có b = ka suy ra $k=\frac{b}{a}.$

Khi a = 5 và b = - 10 ta có $k=\frac{-10}{5}=-2.$

Vậy hệ số tỉ lệ của b đối với a là – 2. Biểu diễn b theo a là b = – 2a.

b) Do b tỉ lệ với a theo hệ số tỉ lệ là – 2 (theo câu a)

Nên a tỉ lệ với b theo hệ số tỉ lệ là $-\frac{1}{2}.$

Vậy hệ số tỉ lệ của a đối với b là $-\frac{1}{2}.$  Biểu diễn a theo b là $a=-\frac{1}{2}b$.

Bài 3 trang 11 SBT Toán 7 Tập 2: Cho x và y là hai đại lượng tỉ lệ thuận với nhau. Hãy tính các giá trị còn thiếu trong bảng sau rồi viết công thức tính y theo x.

Lời giải:

Do x và y là hai đại lượng tỉ lệ thuận với nhau nên ta có:

$\frac{x_1}{y_1}=\frac{x_2}{y_2}=\frac{x_3}{y_3}=\mathrm{...}$

Với x₁ = –3 và y₁ = 9 ta có $\frac{-3}{9}=\frac{x_2}{y_2}=\frac{x_3}{y_3}=\mathrm{...}$  hay $\frac{-1}{3}=\frac{x_2}{y_2}=\frac{x_3}{y_3}=\mathrm{...}$

Khi đó:

• x₂ = -2 thì $\frac{-1}{3}=\frac{-2}{y_2}$  nên y₂ = $\frac{3.\left(-2\right)}{-1}$  = 6;

• x₃ = -1 thì $\frac{-1}{3}=\frac{-1}{y_3}$  nên y₃ = 3;

• x₄ = 1 thì $\frac{-1}{3}=\frac{1}{y_4}$  nên y₄ = $\frac{3.1}{-1}$  = -3;

• x₅ = 2 thì $\frac{-1}{3}=\frac{2}{y_5}$  nên y₅ = $\frac{3.2}{-1}$  = -6.

Vậy ta điền các giá trị còn thiếu trong bảng như sau:

Ta có $\frac{x_1}{y_1}=\frac{x_2}{y_2}=\frac{x_3}{y_3}=\mathrm{...}\frac{-1}{3}$  suy ra ta có công thức tính y theo x là y = –3x.

Vậy công thức tính y theo x là y = –3x.

Giải SBT Toán 7 trang 12 Tập 2

Bài 4 trang 12 SBT Toán 7 Tập 2: Cho biết hai đại lượng P và V tỉ lệ thuận với nhau:

a) Tính các giá trị còn thiếu trong bảng trên.

b) Viết công thức tính P theo V.

Lời giải:

a) Do V và P là hai đại lượng tỉ lệ thuận với nhau nên ta có:

$\frac{V_1}{P_1}=\frac{V_2}{P_2}=\frac{V_3}{P_3}=\mathrm{...}$

Với V₁ = 1 và P₁ = 8,9 ta có $\frac{1}{\mathrm{8,9}}=\frac{V_2}{P_2}=\frac{V_3}{P_3}=\mathrm{...}$

Khi đó:

• V₂ = 2 thì $\frac{2}{P_2}=\frac{1}{\mathrm{8,9}}$  nên P₂ = 8,9 . 2 = 17,8;

• V₃ = 3 thì $\frac{3}{P_3}=\frac{1}{\mathrm{8,9}}$  nên P₃ = 8,9 . 3 = 26,7;

• V₄ = 4 thì $\frac{4}{P_4}=\frac{1}{\mathrm{8,9}}$  nên P₄ = 8,9 . 4 = 35,6;

• V₅ = 5 thì $\frac{5}{P_5}=\frac{1}{\mathrm{8,9}}$  nên P₅ = 8,9 . 5 = 44,5.

Vậy ta điền các giá trị còn thiếu trong bảng như sau:

b) Ta có $\frac{V_1}{P_1}=\frac{V_2}{P_2}=\frac{V_3}{P_3}=\mathrm{...}=\frac{1}{\mathrm{8,9}}$  (theo câu a)

Suy ra $\frac{V}{P}=\frac{1}{\mathrm{8,9}}$  hay P = 8,9V.

Vậy công thức tính P theo V là P = 8,9V.

Bài 5 trang 12 SBT Toán 7 Tập 2: Cho biết x tỉ lệ thuận với y theo hệ số tỉ lệ k và y tỉ lệ thuận với z theo hệ số tỉ lệ q.

a) Hãy tính x theo y, tính y theo z.

b) Hãy tính x theo z.

Lời giải:

a) Do x tỉ lệ thuận với y theo hệ số tỉ lệ k nên ta có x = ky;

Do y tỉ lệ thuận với z theo hệ số tỉ lệ q nên ta có y = qz.

Vậy x = ky và y = qz.

b) Thay y = qz vào x = ky ta được: x = kqz.

Vậy x = kqz.

Bài 6 trang 12 SBT Toán 7 Tập 2: Trong các trường hợp sau, hãy kiểm tra xem hai đại lượng đã cho có tỉ lệ thuận với nhau hay không.

a)

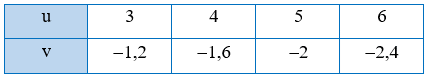
b)

Lời giải:

a) Khi u = 3 và v = -1,2 thì $\frac{u}{v}=\frac{3}{-\mathrm{1,2}}=\frac{30}{-12}=\frac{-5}{2}=-\mathrm{2,5.}$

Khi u = 4 và v = -1,6 thì $\frac{u}{v}=\frac{4}{-\mathrm{1,6}}=\frac{40}{-16}=\frac{-5}{2}=-\mathrm{2,5.}$

Khi u = 5 và v = -2 thì $\frac{u}{v}=\frac{-5}{2}=-\mathrm{2,5.}$

Khi u = 6 và v = -2,4 thì $\frac{u}{v}=\frac{6}{-\mathrm{2,4}}=\frac{60}{-24}=\frac{-5}{2}=-\mathrm{2,5.}$

Khi đó ta có: $\frac{u}{v}=\frac{3}{-\mathrm{1,2}}=\frac{4}{-\mathrm{1,6}}=\frac{5}{-2}=\frac{6}{-\mathrm{2,4}}=-\mathrm{2,5.}$

Vậy u tỉ lệ thuận với v theo hệ số tỉ lệ –2,5.

b) Khi m = -1 và n = 3 thì $\frac{m}{n}=\frac{-1}{3}.$

Khi m = 3 và n = -8 thì $\frac{m}{n}=\frac{3}{-8}=\frac{-3}{8}.$

Ta có $\frac{-1}{3}=\frac{-8}{24}\ne \frac{-3}{8}=\frac{-9}{24}$

Vậy hai đại lượng m và n không tỉ lệ thuận với nhau.

Bài 7 trang 12 SBT Toán 7 Tập 2: Trong các  trường hợp sau, hãy kiểm tra xem hai đại lượng đã cho có tỉ lệ thuận với nhau hay không

a)

b)

Lời giải:

a) Khi x = -4 và y = 8 thì $\frac{x}{y}=\frac{-4}{8}=\frac{-1}{2}=-\mathrm{0,5.}$

Khi x = -3 và y = 6 thì $\frac{x}{y}=\frac{-3}{6}=\frac{-1}{2}=-\mathrm{0,5.}$

Khi x = -2 và y = 4 thì $\frac{x}{y}=\frac{-2}{4}=\frac{-1}{2}=-\mathrm{0,5.}$

Khi x = 1 và y = -2 thì $\frac{x}{y}=\frac{-1}{2}=-\mathrm{0,5.}$

Khi x = 2 và y = -4 thì $\frac{x}{y}=\frac{2}{-4}=\frac{-1}{2}=-\mathrm{0,5.}$

Khi đó ta có: $\frac{x}{y}=\frac{-4}{8}=\frac{-3}{6}=\frac{-2}{4}=\frac{1}{-2}=\frac{2}{-4}=-\mathrm{0,5.}$

Vậy x tỉ lệ thuận với y theo hệ số tỉ lệ –0,5.

b) Khi z = 1 và t = 2 thì $\frac{z}{t}=\frac{1}{2}.$

Khi z = 5 và t = 15 thì $\frac{z}{t}=\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}.$

Ta có $\frac{1}{2}=\frac{3}{6}\ne \frac{1}{3}=\frac{2}{6}$

Vậy z và t không tỉ lệ thuận với nhau.

Bài 8 trang 12 SBT Toán 7 Tập 2: Cúc và Trúc cùng nhau nuôi thỏ, Cúc nuôi 5 con, Trúc nuôi 4 con. Hai bạn bán được tổng cộng 1,8 triệu đồng. Tính số tiền mỗi bạn nhận được nếu chia tỉ lệ theo số thỏ mỗi bạn đã nuôi.

Lời giải:

Gọi số tiền bạn Cúc nhận được là x (triệu đồng), bạn Trúc nhận được là y (triệu đồng).

Do hai bạn bán được tổng cộng 1,8 triệu đồng nên x + y = 1,8.

Vì số tiền mỗi bạn nhận được tỉ lệ theo số thỏ mỗi bạn đã nuôi nên $\frac{x}{5}=\frac{y}{4}.$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{5}=\frac{y}{4}=\frac{x+y}{5+4}=\frac{\mathrm{1,8}}{9}=\mathrm{0,2.}$

Khi đó:

• $\frac{x}{5}=\mathrm{0,2}$  nên x = 0,2 . 5 = 1;

• $\frac{y}{4}=\mathrm{0,2}$  nên y = 0,2 . 4 = 0,8.

Vậy bạn Cúc nhận được 1 triệu đồng, bạn Trúc nhận được 0,8 triệu đồng.

Bài 9 trang 12 SBT Toán 7 Tập 2: Hai lớp 7A và 7B quyên góp được một số sách tỉ lệ thuận với số học sinh của lớp, biết số học sinh của hai lớp lần lượt là 32 và 36. Lớp 7A quyên góp được ít hơn lớp 7B 8 quyển sách. Hỏi mỗi lớp quyên góp được bao nhiêu quyển sách?

Lời giải:

Gọi số sách lớp 7A quyên góp là x (quyển), số sách lớp 7B quyên góp là y (quyển).

Hai lớp 7A và 7B quyên góp được số sách tỉ lệ thuận với số học sinh của lớp, mà số học sinh của hai lớp lần lượt là 32 và 36 nên ta có $\frac{x}{32}=\frac{y}{36}.$

Do lớp 7A quyên góp được ít hơn lớp 7B 8 quyển sách nên y - x = 8.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{32}=\frac{y}{36}=\frac{y-x}{36-32}=\frac{8}{4}=2.$

Khi đó:

• $\frac{x}{32}=2$  nên x = 2 . 32 = 64;

• $\frac{y}{36}=2$  nên y = 2 . 36 = 72.

Vậy lớp 7A quyên góp được 64 quyển sách, lớp 7B quyên góp được 72 quyển sách.

Giải SBT Toán 7 trang 13 Tập 2

Bài 10 trang 13 SBT Toán 7 Tập 2: Một tam giác có ba cạnh tỉ lệ với 5; 12; 13 và có chu vi là 120 cm. Tính độ dài các cạnh của tam giác đó.

Lời giải:

Gọi x, y, z (cm) lần lượt là độ dài 3 cạnh của một tam giác.

Do chu vi tam giác là 120 cm nên x + y + z = 120.

Do tam giác có ba cạnh tỉ lệ với 5; 12; 13 nên $\frac{x}{5}=\frac{y}{12}=\frac{z}{13}.$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{5}=\frac{y}{12}=\frac{z}{13}=\frac{x+y+z}{5+12+13}=\frac{120}{30}=4.$

Khi đó:

• $\frac{x}{5}=4$  nên x = 4 . 5 = 20;

• $\frac{y}{12}=4$  nên y = 4 . 12 = 48;

• $\frac{z}{13}=4$  nên y = 4 . 13 = 52.

Vậy độ dài 3 cạnh của tam giác là: 20 cm, 48 cm, 52 cm.

Bài 11 trang 13 SBT Toán 7 Tập 2: Tùng, Huy và Minh cùng trồng hoa cúc trong chậu để chuẩn bị bán tết. Tùng trồng được 6 chậu hoa, Huy trồng được 4 chậu hoa và Minh trồng được 5 chậu hoa. Bác Tư giúp các bạn bán hết số chậu hoa được tổng cộng 1,5 triệu đồng. Ba bạn quyết định chia tiền tỉ lệ với số chậu hoa trồng được. Hỏi mỗi bạn được chia bao nhiêu tiền?

Lời giải:

Gọi số tiền bạn Tùng, Huy, Minh lần lượt nhận được là x, y, z (triệu đồng).

Do tổng số tiền 3 bạn nhận được khi bán hết chậu hoa là 1,5 triệu đồng nên ta có: $\frac{x}{6}=\frac{y}{4}=\frac{z}{5}.$

x + y + z = 1,5.

Do số tiền mỗi bạn nhận được tỉ lệ với số chậu hoa trồng được nên ta có:

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{x}{6}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{6+4+5}=\frac{\mathrm{1,5}}{15}=\mathrm{0,1.}$

Khi đó:

• $\frac{x}{6}=\mathrm{0,1}$  nên x = 0,1 . 6 = 0,6 (triệu đồng) = 600 nghìn đồng;

• $\frac{y}{4}=\mathrm{0,1}$  nên y = 0,1 . 4 = 0,4 (triệu đồng) = 400 nghìn đồng;

• $\frac{z}{5}=\mathrm{0,1}$  nên y = 0,1 . 5 = 0,5 (triệu đồng) = 500 nghìn đồng.

Vậy số tiền mỗi bạn nhận được là: bạn Tùng 600 nghìn đồng, bạn Huy 400 nghìn đồng, bạn Minh 500 nghìn đồng.

Bài 12 trang 13 SBT Toán 7 Tập 2: Cho biết mỗi lít nước tương có khối lượng 1,2 kg.

a) Giả sử x lít nước tương có khối lượng y kg. Hãy viết công thức tính y theo x.

b) Tính thể tích của 800 g nước tương.

Lời giải:

a) Vì 1 lít nước có khối lượng 1,2 kg nên x lít nước có khối lượng 1,2x kg.

Khi đó: y = 1,2x.

Vậy công thức tính y theo x là y = 1,2x.

b) Đổi: 800 g = 0,8 kg.

Do y = 1,2x nên $x=\frac{y}{\mathrm{1,2}}$ .

Do có 0,8g nước nên $x=\frac{\mathrm{0,8}}{\mathrm{1,2}}=\frac{8}{12}=\frac{2}{3}\approx \mathrm{0,67.}$

Vậy thể tích của 800 g nước tương là khoảng 0,67 lít.

Xem thêm lời giải sách bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài tập cuối chương 5

Bài 1: Tỉ lệ thức - Dãy tỉ số bằng nhau

Bài 3: Đại lượng tỉ lệ nghịch

Bài tập cuối chương 6

Bài 1: Biểu thức số, biểu thức đại số