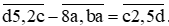Sách bài tập Toán 6 Ôn tập chương 7
Bài tập trắc nghiệm
Bài 1 trang 37 sách bài tập Toán lớp 6 Tập 2: Chữ số hàng phần trăm của số thập phân –1 435,672 là:
A. 4
B. 3
C. 7
D. 2
Lời giải:
Các chữ số phần thập phân viết bên phải dấu phẩy, bao gồm: phần mười, phần trăm, phần nghìn,…
Chữ số hàng phần trăm là chữ số thứ 2 sau dấu phẩy.
Chữ số thứ 2 sau dấu phẩy của số –1 435,672 là 7.
Vậy chữ số hàng phần trăm của số thập phân –1 435,672 là: C. 7.
Bài 2 trang 37 sách bài tập Toán lớp 6 Tập 2: Trong các câu sau, câu nào sai?
A. Tổng của hai số thập phân dương là một số thập phân dương
B. Tích của hai số thập phân dương là một số thập phân dương
C. Hiệu của hai số thập phân dương là một số thập phân dương
D. Thương của hai số thập phân dương là một số thập phân dương
Lời giải:
Khẳng định A, B, D đúng.
Khẳng định C sai. Chẳng hạn: 0,25 – 2,15 = –1,9. Hiệu của hai số thập phân dương có thể là số thập phân âm.
Vậy khẳng định sai là C.
Bài 3 trang 37 sách bài tập Toán lớp 6 Tập 2: Trong các câu sau, câu nào đúng?
A. Hiệu của hai số thập phân âm là một số thập phân âm
B. Tổng của hai số thập phân âm là một số thập phân âm
C. Tích của hai số thập phân âm là một số thập phân âm
D. Thương của hai số thập phân âm là một số thập phân âm
Lời giải:
- Khẳng định A sai. Chẳng hạn: (–1,3) – (–2,4) = 1,1. Hiệu của hai số thập phân âm có thể là số thập phân dương.
- Khẳng định B đúng.
- Khẳng định C sai vì tích của hai số thập phân âm là một số thập phân dương.
Chẳng hạn: (–12) . (–5) = 12 . 5 = 60.
- Khẳng định D sai vì thương của hai số thập phân âm là một số thập phân dương.
Chẳng hạn: (–45) : (–5) = 45 : 5 = 9.
Vậy khẳng định đúng là B.
A. 131,29
B. 131,30
C. 131,31
D. 130
Lời giải:
Làm tròn số 131,2956 đến chữ số thập phân thứ hai:
- Chữ số thập phân thứ hai của số 131,2956 là 9.
- Chữ số bên phải liền nó là 5 nên chữ số hàng phần trăm tăng lên một đơn vị (các chữ số tính từ hàng cao nhất đến chữ số thập phân thứ hai là 131,29 cộng thêm một đơn vị ở chữ số thập phân thứ hai là 131,30) và bỏ các chữ số từ chữ số thập phân thứ ba trở đi.
Do đó số 131,2956 làm tròn đến chữ số thập phân thứ hai là 131,30.
Vậy chọn đáp án B. 131,30.
Bài 5 trang 37 sách bài tập Toán lớp 6 Tập 2: Tích 214,9 . 1,09 là:
A. 234, 241
B. 209,241
C. 231,124
D. –234,241
Lời giải:
Phép tính 214,9 . 1,09 là phép nhân hai số thập phân dương, ta làm như sau:
- Bỏ dấu phẩy ở các số thập phân rồi thực hiện phép nhân hai số tự nhiên.
Ta tính được: 2 149 . 109 = 234 241.
- Phần thập phân ở cả hai thừa số có tất cả 3 chữ số.
- Dùng dấu phẩy tách ở tích ra 3 chữ số từ phải sang trái, ta được 234,241.
Do đó 214,9 . 1,09 = 234,241.
Vậy tích 214,9 . 1,09 là: A. 234, 241.
A. 31%
B. 19%
C. 20%
D. 21%
Lời giải:
Gọi a là lương ban đầu của công nhân đó.
Mức lương được tăng thêm so với lương ban đầu là: a. 10%
Sau lần tăng thứ nhất, lương người đó là:
a + a . 10% = (1 + 10%) . a = 1,1 . a
Mức lương tăng lần thứ hai tăng thêm so với lương tăng lần thứ nhất là:
1,1 . a. 10% = 0,11 . a
Sau lần tăng thứ hai, lương người đó là:
1,1 . a + 0,11 . a = (1,1 + 0,11) . a = 1,21 . a
Tỉ số phần trăm lương mới so với lương cũ là:
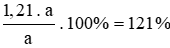
Sau hai lần tăng lương, mức lương đã tăng là:
121% – 100% = 21%
Vậy chọn đáp án là: D. 21%.
Bài tập
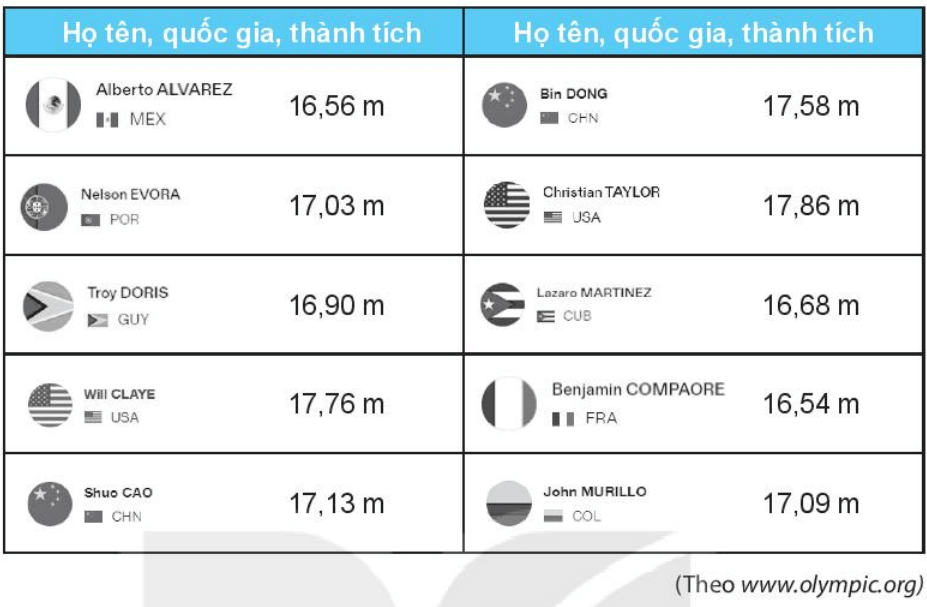
a) Sắp xếp theo thứ tự từ cao xuống thấp kết quả thi đấu của 10 vận động viên này.
b) Em hãy cho biết huy chương vàng, bạc, đồng thuộc về các vận động viên nào.
Lời giải:
a) Sắp xếp thành tích môn nhảy ba bước nam của 10 vận động viên theo thú tự giảm dần, ta so sánh từ hàng phần số nguyên đến phần thập phân (từ chữ số hàng cao nhất đến chữ số hàng thấp nhất).
Vì 17,86 > 17,76 > 17,58 > 17,13 > 17,09 > 17,03 > 16,90 > 16,68 > 16,56 > 16,54 nên ta có được:
Kết quả sắp xếp theo thứ tự từ cao xuống thấp của 10 vận động viên này là:
Christian TAYLOR; Will CLAYE; Bin DONG; Shuo CAO; John MURILLO; Nelson EVORA; Troy DORIS; Lazaro MARTINEZ; Alberto ALVAREZ; Benjamin COMPAORE.
b) Huy chương vàng thuộc về người có thành tích cao nhất là vận động viên Christian TALOR (17,86 m);
Huy chương bạc thuộc về người có thành tích cao thứ hai là vận động viên Will CLAYE (17,76 m);
Huy chương đồng thuộc về người có thành tích cao thứ ba là vận động viên Bin DONG (17,58 m).
Vậy huy chương vàng, bạc, đồng lần lượt thuộc về các vận động viên Christian TALOR, Will CLAYE, Bin DONG.
Bài 7.36 trang 38 sách bài tập Toán lớp 6 Tập 2:a) So sánh hai số: a = 0,29 và b = 0,3;
b) Tìm một số thập phân x thỏa mãn điều kiện a < x < b;
c) Có hay không 9 số thập phân x thỏa mãn điều kiện a < x < b?
Lời giải:
a)
- Phần số nguyên của hai số 0,29 và 0,3 đều là 0;
- Phần thập phân có chữ số hàng phần mười của 0,29 và 0,3 lần lượt là 2 và 3.
Vì 2 < 3 nên 0,29 < 0,3.
Vậy a < b.
b) Ta có: 0,29 = 0,290; 0,3 = 0,300
Tìm một số thập phân nằm giữa hai số thập 0,290 và 0,300:
- Ta tìm một số nằm giữa 290 và 300. Chẳng hạn: chọn số 295.
- Thêm phần nguyên và dấu phẩy vào ta được số 0,295.
Do đó một số thập phân nằm giữa hai số thập 0,29 và 0,3 là số 0,295.
Vậy một số thập phân thỏa mãn a < x < b là số 0,295.
c) Tương tự như câu b. Ta tìm 9 số thập phân nằm giữa hai số thập 0,290 và 0,300:
- Ta tìm 9 số nằm giữa 290 và 300. Ta chọn ra các số 291; 292; 293; 294; 295; 296; 297; 298; 299.
- Thêm phần nguyên và dấu phẩy vào các số trên ta được: 0,291; 0,292; 0,293; 0,294; 0,295; 0,296; 0,297; 0,298; 0,299.
Do đó 9 số thập phân nằm giữa hai số thập 0,29 và 0,3 là số 0,291; 0,292; 0,293; 0,294; 0,295; 0,296; 0,297; 0,298; 0,299.
Vậy 9 số thập phân thỏa mãn a < x < b là x ∈ {0,291; 0,292; 0,293; 0,294; 0,295; 0,296; 0,297; 0,298; 0,299}.
Nhận xét:
Ngoài 9 số ta chọn ở trên, ta cố thể chọn vô số các số thập phân khác.
Ví dụ: Ta có: 0,29 = 0,2900; 0,3 = 0,3000
Tìm một số thập phân nằm giữa hai số thập 0,2900 và 0,3000:
- Ta có thể tìm được nhiều số nằm giữa 2 900 và 3 000 là: 2 901; 2 902;…
- Thêm phần nguyên và dấu phẩy vào ta được các số tương ứng là: 0,2901; 0,2902;…
Khi ta càng tăng chữ số 0 ở bên phải các chữ số phần thập phân, ta tìm được càng nhiều chữ số thập phân nằm ở giữa hai số thập phân cho trước.
Do đó, có vô số số thập phân nằm giữa hai số thập phân.
Bài 7.37 trang 38 sách bài tập Toán lớp 6 Tập 2: Tính nhẩm (theo mẫu):
7,98 + 2,48 = (7,98 + 0,02) + (2,48 – 0,02) = 8 + 2,46 = 10,46.
Lời giải:
Để tính nhẩm các phép tính trên, ta áp dụng tính chất giao hoán, kết hợp các số “đẹp”, thường thì kết quả trong nhóm là số nguyên để tiện cho việc tính toán.
a) 51,99 + 21,55 = (51,99 + 0,01) + ( 21,55 – 0,01) = 52 + 21,54 = 73,54;
b) 17,31 – 1,96 = (17,31 + 0,04 ) – (1,96 + 0,04) = 17,35 – 2 = 15,35;
c) 16,78 – 12,99 = (16,78 + 0,01) – (12,99 + 0,01) = 16,79 – 13 = 3,79;
d) –15,95 – 31,72 = –(15,95 + 31,72) = –[(15,95+ 0,05) + (31,72 – 0,05)]
= –(16 + 31,67) = –47,67.
Bài 7.38 trang 38 sách bài tập Toán lớp 6 Tập 2: Tính giá trị của các biểu thức sau:
b) 5,25 . 4,1 + (–2,05) . 16,4 + 2,625 . 8,2.
Lời giải:
a) Cách 1: Thực hiện phép tính theo thứ tự: nhân chia trước, cộng trừ sau.
0,62 . 351 + (–35,1) : 4
= 217,62 + (–8,775)
= 217,62 – 8,775
= 208,845.
Cách 2: Áp tính chất phân phối sau đó tính giá trị biểu thức theo thứ tự thực hiện phép tính.
0,62 . 351 + (–35,1) : 4
= 0,62 . 351 – 351 : 40
= 0,62 . 351 – 351. 0,025
= 351. (0,62 – 0,025) (Tính chất phân phối)
= 351 . 0,595
= 208,845.
b) Cách 1: Thực hiện phép tính theo thứ tự: nhân chia trước, cộng trừ sau.
5,25 . 4,1 + (–2,05) . 16,4 + 2,625 . 8,2
= 21,525 + (–33,62) + 21,525
= –12,095 + 21,525
= 21,525 – 12,095
= 9,43.
Cách 2: Áp tính chất phân phối sau đó tính giá trị biểu thức theo thứ tự thực hiện phép tính.
5,25 . 4,1 + (–2,05) . 16,4 + 2,625 . 8,2
= 5,25 . 4,1 + (–2,05) . 4 . 4,1 + 2,625 . 2 . 4,1
= 4,1 . [5,25 + (–2,05) . 4 + 2,625 . 2] (Tính chất phân phối)
= 4,1 . (5,25 + (–8,2) + 5,25)
= 4,1 . 2,3
= 9,43.
Lời giải:
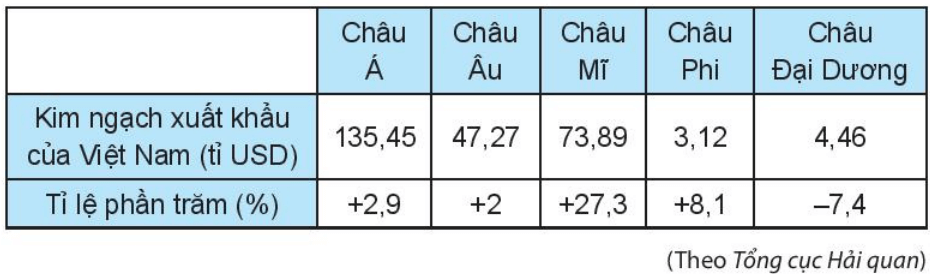
a) Tổng kim ngạch xuất khẩu của Việt Nam năm 2019 là:
135,45 + 47,27 + 73,89 + 3,12 + 4,46 = 264,19 (tỉ USD)
Vậy tổng kim ngạch xuất khẩu của Việt Nam năm 2019 là 264,19 tỉ USD.
b) Kim ngạch xuất khẩu với châu Mĩ năm 2019 là 73,89 tỉ USD và tăng 27,3% so với năm 2018.
Khi đó, kim ngạch xuất khẩu với châu Mĩ sau khi tăng 27,3% là:
100% + 27,3% = 127,3%.
Như vậy, 73,89 tỉ USD bằng 127,3% kim ngạch xuất khẩu với châu Mĩ năm 2018.
Kim ngạch xuất khẩu của Việt Nam với châu Mĩ năm 2018 là:
73,89 : 127,3% = 58,043 990 57 (tỉ USD)
Làm tròn số 58,043 990 57 đến hàng phần trăm, ta được: 58,04.
Vậy kim ngạch xuất khẩu của Việt Nam với châu Mĩ năm 2018 là 58,04 tỉ USD.
(Theo interbrand.com)
Lời giải:
a) Tỉ số phần trăm giá trị thương hiệu Apple năm 2019 so với giá trị thương hiệu Apple năm 2013 là:
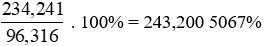
Làm tròn số 243,200 5067 đến chữ số thập phân thứ nhất, ta được: 243,2.
Vậy tỉ số phần trăm giá trị thương hiệu Apple năm 2019 so với giá trị thương hiệu Apple năm 2013 là 243,2%.
b) Giá trị thương hiệu Apple năm 2019 là 234,241 tỉ USD và tăng 9% so với năm 2018.
Khi đó, giá trị thương hiệu Apple sau khi tăng 9% là:
100% + 9% = 109%.
Như vậy, giá trị thương hiệu Apple năm 2019 là 234,241 tỉ USD và bằng 109% năm 2018.
Giá trị thương hiệu Apple năm 2018 là:
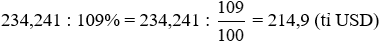
Vậy giá trị thương hiệu Apple năm 2018 là 214,9 tỉ USD.
(Theo Tổng cục Thống kê)
Lời giải:
Tỉ số phần trăm sản lượng gạo xuất khẩu của Việt Nam trong năm 2019 so với năm 2018 là:
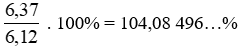
Làm tròn số 104,08 496… đến hàng phần mười, ta được: 104,1.
Tổng sản lượng gạo xuất khẩu của Việt Nam trong năm 2019 tăng số phần trăm so với năm 2018 là:
104,1% – 100% = 4,1%
Tỉ số phần trăm sản lượng gạo xuất khẩu của Việt Nam trong năm 2019 so với năm 2018 là:
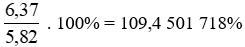
Làm tròn số 109,4 501 718 đến hàng phần mười, ta được: 109,5.
Tổng sản lượng gạo xuất khẩu của Việt Nam trong năm 2019 tăng số phần trăm so với năm 2017 là:
109,5% – 100% = 9,5%
Vậy tổng sản lượng gạo xuất khẩu của Việt Nam trong năm 2019 tăng số phần trăm so với năm 2018 và so với năm 2017 lần lượt là 4,1% và 9,5%.
Lời giải:
Vì số chữ số ở phần thập phân là như nhau nên ta có thể bỏ đi dấu phẩy và đưa bài toán trở thành:
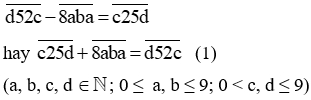
Vế phải phải là số có 4 chữ số nên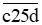 
< 10 000 nên c < 2
Do đó c = 1.
Khi đó (1) trở thành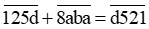 
(2)
Ta thấy chữ số hàng nghìn của các số hạng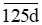 
và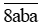 
của vế trái của (2) lần lượt là 1 và 8.
Do đó vế phái của (2) lớn hơn 1 000 + 8 000 = 9 000 và vế phải có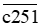 
< 10 000.
Do đó d = 9.
Khi đó (2) trở thành
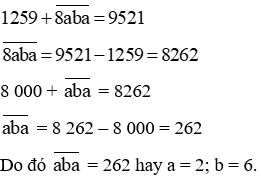
Từ đó suy ra: a = 2; b = 6; c = 1; d = 9.
Vậy phép trừ đúng là: 95,21 – 82,62 = 12,59.
Xem thêm các bài giải SBT Toán 6 Kết nối tri thức hay, chi tiết khác:
Bài 31. Một số bài toán về tỉ số và tỉ số phần trăm