Sách bài tập Toán 6 Bài 34: Đoạn thẳng. Độ dài đoạn thẳng
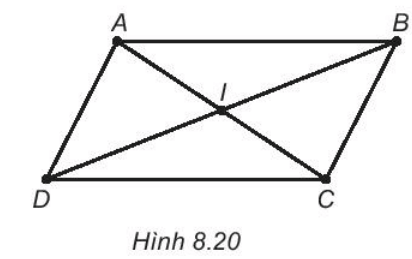
Bài 8.26 trang 49 sách bài tập Toán lớp 6 Tập 2: Xem Hình 8.20.
Dùng compa để kiểm tra sự bằng nhau của hai đoạn thẳng trong mỗi cặp: AB và CD; AD và BC.
Lời giải:
Lời giải:
* Kiểm tra sự bằng nhau của AB và CD:
- Đặt tâm của compa vào một đầu mút của đoạn thẳng AB, đầu bút của compa chạm vào mút còn lại.
- Giữ khoảng cách giữ tâm và đầu bút.
- Tiếp tục đặt tâm của compa vào một đầu mút của đoạn thẳng CD. Kiểm tra xem đầu bút của compa có chạm vào mút còn lại hay không.
Ta thấy: đầu bút của compa chạm vào mút còn lại nên AB = CD.
* Kiểm tra sự bằng nhau của AD và BC:
- Đặt tâm của compa vào một đầu mút của đoạn thẳng AD, đầu bút của compa chạm vào mút còn lại.
- Giữ khoảng cách giữ tâm và đầu bút.
- Tiếp tục đặt tâm của compa vào một đầu mút của đoạn thẳng BC. Kiểm tra xem đầu bút của compa có chạm vào mút còn lại hay không.
Ta thấy: đầu bút của compa chạm vào mút còn lại nên AD = BC.
Lời giải:
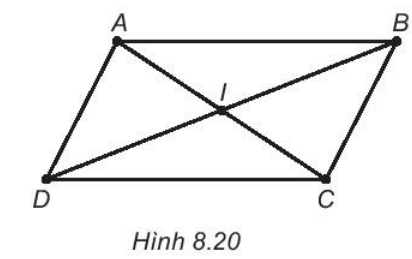
* Đo độ dài cạnh IA:
Đặt thước sao cho mép thước dọc theo cạnh IA. Một trong hai điểm I và A trùng với vạch 0.
Chẳng hạn: cho điểm I trùng với vạch 0, điểm A trùng với vạch bao nhiêu thì đó chính là độ dài của đoạn thẳng IA.
Do đó, độ dài đoạn thẳng IA = 18 mm.
* Đo độ dài cạnh IB:
Đặt thước sao cho mép thước dọc theo cạnh IB. Một trong hai điểm I và B trùng với vạch 0.
Chẳng hạn: cho điểm I trùng với vạch 0, điểm B trùng với vạch bao nhiêu thì đó chính là độ dài của đoạn thẳng IB.
Do đó, độ dài đoạn thẳng IB = 27 mm.
* Đo độ dài cạnh IC:
Đặt thước sao cho mép thước dọc theo cạnh IC. Một trong hai điểm I và C trùng với vạch 0.
Chẳng hạn: cho điểm I trùng với vạch 0, điểm C trùng với vạch bao nhiêu thì đó chính là độ dài của đoạn thẳng IC.
Do đó, độ dài đoạn thẳng IC = 18 mm.
* Đo độ dài cạnh ID:
Đặt thước sao cho mép thước dọc theo cạnh ID. Một trong hai điểm I và D trùng với vạch 0.
Chẳng hạn: cho điểm I trùng với vạch 0, điểm D trùng với vạch bao nhiêu thì đó chính là độ dài của đoạn thẳng ID.
Do đó, độ dài đoạn thẳng ID = 27 mm.
Vậy IA = IC = 18 mm; IB = ID = 27 mm.
Lời giải:
Hai điểm A và B cách nhau một khoảng bằng 8 cm hay độ dài đoạn thẳng AB = 8 cm.
Gọi đoạn thẳng đơn vị có độ dài 2 cm là đoạn thẳng MN.
Khi đó, MN = 2 cm.
Ta có hình vẽ:

Ta có: 8 = 4 . 2 nên AB = 4 . MN.
Do đó độ dài đoạn thẳng AB có độ dài bằng 4 lần độ dài đoạn thẳng MN.
Vậy nếu ta chọn một đoạn thẳng có độ dài 2 cm làm đơn vị độ dài thì đoạn AB bằng 4 đơn vị độ dài đoạn thẳng có độ dài 2 cm.
a) Hai điểm O và B nằm cùng phía đối với điểm A;
b) Hai điểm O và B nằm khác phía đối với điểm A.
Lời giải:
Điểm B nằm cách A một khoảng bằng 3 cm hay độ dài AB = 3 cm.
a) Điểm B nằm trên đường thẳng OA hay ba điểm O, A, B cùng nằm trên một đường thẳng.
Mà hai điểm O và B nằm cùng phía đối với điểm A.
Nên điểm B nằm giữa hai điểm O và A.
* Cách xác định điểm B:
- Vẽ đoạn thẳng OA = 7 cm;
- Trên đoạn thẳng OA lấy điểm B sao cho AB = 3 cm.
Ta có hình vẽ:

b) Điểm B nằm trên đường thẳng OA hay ba điểm O, A, B cùng nằm trên một đường thẳng.
Mà hai điểm O và B nằm khác phía đối với điểm A.
Nên điểm A nằm giữa hai điểm O và B.
* Cách xác định điểm B:
- Vẽ đoạn thẳng OA = 7 cm;
- Trên tia đối của tia AO, lấy điểm B sao cho AB = 3 cm.
Ta có hình vẽ:

Lời giải:
Vì S là một điểm thuộc đoạn thẳng PQ nên S nằm giữa hai điểm P và Q (như hình vẽ).

Ta có: SP + SQ = PQ
Do đó PQ = 3 + 5 = 8 (cm)
Vậy PQ = 8 cm.
Lời giải:
Vì M là một điểm thuộc đoạn thẳng EF nên điểm M nằm giữa hai điểm E và F (như hình vẽ).

Ta có: EM + MF = EF
EM + 5 = 10
EM = 10 – 5
EM = 5 cm.
Mà MF = 5 cm.
Vậy EM = EF.
Lời giải:

Ta có: EF = EM + MN + NF
12 = 4 + MN + 5
12 = 9 + MN
MN = 12 – 9
MN = 3 cm.
Vậy MN = 3 cm.
Lời giải:
Cây gậy dài 1,5 m nên mỗi lần đặt gậy tương ứng với 1,5 m.
Do đó 5 lần đặt gậy tương ứng với độ dài là:
5 . 1,5 = 7,5 (m).
Chiều rộng của lớp học bằng 5 lần đặt cây gậy 1,5 m thì khoảng cách còn lại là 1 m.
Khi đó, chiều rộng của lớp học là:
7,5 + 1 = 8,5 (m).
Vậy chiều rộng của lớp học là 8,5 m.
Lời giải:
Ba điểm A, B, C thẳng hàng thì có 3 trường hợp có thể xảy ra:
- Trường hợp 1: Điểm B nằm giữa hai điểm A và C.
Khi đó, AC = BA + BC.
- Trường hợp 2: Điểm C nằm giữa hai điểm A và B.
Khi đó, AB = AC + CB.
- Trường hợp 3: Điểm A nằm giữa hai điểm B và C.
Khi đó, BC = AB + AC. Đây là hệ thức đã cho.
Vậy BC = AB + AC thì trường hợp 3 xảy ra, tức là điểm A nằm giữa hai điểm B và C.
Lời giải:
* Cách vẽ:
- Vẽ đoạn thẳng AB = 5 cm.
- Trên đoạn thẳng AB lấy AC = 2 cm.
* Ta có hình vẽ:

Theo đề bài: AC = 2 cm; AB = 3 cm và BC = 5 cm.
Ta thấy BC = AB + AC (vì 5 = 3 + 2)
Do đó, điểm A nằm giữa hai điểm B và C.
Vậy trong ba điểm A, B, C thì điểm A nằm giữa hai điểm B và C.
Xem thêm các bài giải SBT Toán 6 Kết nối tri thức hay, chi tiết khác:
Bài 33. Điểm nằm giữa hai điểm. Tia

