Giải SBT Toán 6 (Cánh diều) Bài ôn tập cuối chương 2

Sách bài tập Toán 6 Bài ôn tập cuối chương 2

Bài 61 trang 87 sách bài tập Toán lớp 6 Tập 1: Tính một cách hợp lí:

a) (2 021 – 39) + [(-21) + (-61)];

b) (-625) – {(-547) – 352 – [(-147) – (-735) + (2 200 + 65)]};

c) (-16).125.[(-3).2²].5³ – 2.10⁶;

d) (134 – 34).(-28) + 72.[(-55) – 45].

Lời giải:

a) (2 021 – 39) + [(-21) + (-61)]

= 2 021 + (-39) + (-21) + (-61)

= [2 021 + (-21)] + [(-39) + (-61)]

= 2 000 + (-100)

= 2 000 – 100

= 1 900.

b) (-652) – {(-547) – 352 – [(-147) – (-735) + (2 200 + 65)]}

= (-652) – {(-547) – 352 – [(-147) + 735 + 2 200 + 65]}

= (-652) – {(-547) – 352 – [(-147) + (735 + 65) + 2 200]}

= (-652) – {(-547) – 352 – [(-147) + 800 + 2 200]}

= (-652) – {(-547) – 352 – [(-147) + 3 000]}

= (-652) – {(-547) – 352 + 147 - 3 000}

= (-652) – {[(-547) +147] + [(-352) + (- 3 000)]}

= (-652) – {(-400) + (- 3 352)}

= (-652) – {(- 3 752)}

= (-652) + 3 752

= 3 100.

c) (-16).125.[(-3).2²].5³ – 2.10⁶

= (-16).125.(-3).4.125 – 2.10⁶

= (-2).8.125.(-3).4.125 – 2.10⁶

= (-2).4.125.8.125.(-3) – 2.10⁶

= (-1 000).1 000.(-3) – 2.10⁶

= 3.106 – 2.10⁶

= 10⁶.(3 – 2)

= 10⁶.

d) (134 – 34).(-28) + 72.[(-55) – 45]

= 100.(-28) + 72.(-100)

= 100(-28) + (-72).100

= 100.[(-28) + (-72)]

= 100.(-100)

= - 10 000.

Bài 62 trang 87 sách bài tập Toán lớp 6 Tập 1: Tìm số nguyên x, biết:

a) (-300):20 + 5.(3x – 1) = 25;

b) (5.13)^x = 25.(5³ + 4.11)² : (3⁴ – 3⁵:3³ + 97) (x  0);

c) (x – 5)(3x – 6) = 0;

d) (2x + 1)².(x – 6) > 0;

e) (x + 1).(x – 4) < 0.

Lời giải:

a) (-300):20 + 5.(3x – 1) = 25

(-15) + 5.(3x – 1) = 25

5.(3x – 1) = 25 – (-15)

5.(3x – 1) = 40

3x – 1 = 8

3x = 9

x = 3.

Vậy x = 3.

b) (5.13)^x = 25.(5³ + 4.11)² : (3⁴ – 3⁵:3³ + 97) (x  0)

65^x = 25.(125 + 44)² : (81 – 3² + 97)

65^x = 25.169² : (81 – 9 + 97)

65^x = 25.169² : 169

65^x = 25.169

65^x = 5².13²

65^x = (5.13)²

65^x = (65)²

x = 2 (thỏa mãn điều kiện)

Vậy x = 2.

c) (x – 5)(3x – 6) = 0

TH1: x – 5 = 0

x = 5.

TH2: 3x – 6 = 0

3x = 6

x = 2.

Vậy x = 5 hoặc x = 2.

d) (2x + 1)².(x – 6) > 0

Vì x là số nguyên nên (2x + 1)² > 0 nên để (2x + 1)².(x – 6) > 0 thì x – 6 > 0 khi x > 6.

Vậy x ∈ {7; 8; 9; …}.

e) (x + 1).(x – 4) < 0.

Ta có x + 1 > x – 4

Mà x + 1 và x – 4 trái dấu 

Nên x + 1 > 0 và x – 4 < 0

Suy ra x > - 1 và x < 4

Hay – 1 < x < 4.

Do x là số nguyên nên x ∈ {0; 1; 2; 3}.

Vậy x ∈ {0; 1; 2; 3}.

Bài 63 trang 87 sách bài tập Toán lớp 6 Tập 1: Tìm các giá trị thích hợp của chữ số a, sao cho:

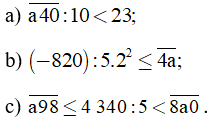
Lời giải:

a) Nhân cả hai vế với 10, ta được:

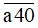 < 23.10 = 230

Do đó a chỉ có thể bằng 1.

Vậy a = 1.

b) Do (-820):5.2² < 0 mà 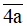 > 0 nên (-820):5.2² ≤  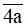luôn đúng.

Suy ra a ∈ .

Vậy a ∈ .

c)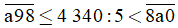 

Ta có 4 340:5 = 868

Khi đó ta có: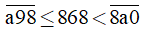 

Suy ra a < 8 và a > 6 hay 6 < a < 8.

Mà a là chữ số nên a = 7.

Vậy a = 7.

Bài 64 trang 87 sách bài tập Toán lớp 6 Tập 1: Tính A – B, biết rằng A là tích của các số nguyên âm chẵn có một chữ số và B là tổng của các số nguyên dương lẻ có hai chữ số.

Lời giải:

Các số nguyên âm chẵn có một chữ số là: - 2; - 4; - 6; - 8.

Khi đó A = (-2).(-4).(-6).(-8)

= 384.

Các số nguyên lẻ có hai chữ số là: 11; 13; 15; …; 99.

B = 11 + 13 + 15 + … + 97 + 99

= (11 + 99) + (13 + 97) + …+ (53 + 57) + 55

= 110 + 110 + … + 110 + 55 (22 số 110)

= 110.22 + 55

= 2 420 + 55

= 2 475.

Suy ra A – B = 384 – 2 475 = - 2091.

Vậy A – B = - 2 091.

Bài 65 trang 87 sách bài tập Toán lớp 6 Tập 1: Bạn Nam muốn điền các số 1; 2; 3; 4; 5; 6; 8; 9 vào bảng bên sao cho tổng các số ở mỗi hàng, mỗi cột và mỗi đường chéo bằng nhau. Tính tổng bốn số ở bốn ô được tô đậm.

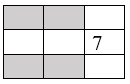
Lời giải:

Tổng các số ở 9 ô là: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45.

Tổng các số ở mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau và bằng 45:3 = 15.

Tổng các số ở hai hàng có ô được tô đậm là: 15.2 = 30.

Ở cột thứ ba, tổng của hai số ở hai ô trắng còn lại là: 15 – 7 = 8.

Do đó, tổng bốn số ở bốn ô tô đậm là: 30 – 8 = 22.

Vậy tổng bốn số ở bốn ô tô đậm là 22.

Bài 66 trang 87 sách bài tập Toán lớp 6 Tập 1: Cho bảng 3 x 3 ô vuông.

a) Viết 9 số nguyên khác 0 vào 9 ô của bảng. Biết rằng tích các số ở mỗi dòng đều là số nguyên âm. Chứng tỏ rằng luôn tồn tại một cột mà tích các số ở cột ấy là số nguyên âm.

b) Có thể điền được hay không 9 số nguyên vào 9 ô của bảng sao cho tổng các số ở ba dòng lần lượt bằng -15; -18; 78 và tổng các số ở ba cột lần lượt bằng 24; -12; 65?

Lời giải:

a) Giả sử trong cả ba cột, tích các số ở mỗi cột đều là số nguyên dương thì tích 9 số của bảng là số nguyên dương (1).

Theo đề bài tích các số ở mỗi dòng là số nguyên âm nên tích các số ở bảng là số nguyên âm, mâu thuẫn với (1).

Vậy phải tồn tại một cột mà tích các số ở cột ấy là số nguyên âm.

b) Không thể điền được.

Vì do tổng của 9 số của bảng tính theo tổng các số ở ba dòng bằng (-15) + (-18) + 78 = 45 là một số chia hết cho 3. Trong khi tổng 9 số của bảng tính theo tổng các số ở ba cột bằng 24 + (-12) + 65 = 77 không chia hết cho 3.

Bài 67 trang 88 sách bài tập Toán lớp 6 Tập 1: Chứng tỏ rằng với mọi số nguyên n:

a) n(n + 1)(n + 2) chia hết cho 2 và 3.

b) n(n + 1)(n + 2)(n + 3) chia hết cho 3 và 8.

Lời giải:

a)

+) Nếu n chẵn thì n chia hết cho 2 nên n(n + 1)(n + 2) chia hết cho 2.

Nếu n lẻ thì n + 1 chia hết cho 2 nên n(n + 1)(n + 2) chia hết cho 2.

Suy ra n(n + 1)(n + 2) chia hết cho 2 với mọi số nguyên n.

+) Nếu n chia hết cho 3 thì n(n + 1)(n + 2) chia hết cho 3.

Nếu n chia cho 3 dư 1 thì n có dạng n = 3k + 1. Khi đó n + 2 = 3k + 3 = 3(k+1) chia hết cho 3 nên n(n + 1)(n + 2) chia hết cho 3.

Nếu n chia cho 3 dư 2 thì n có dạng n = 3k + 2. Khi đó n + 1 = 3k + 2 + 1 = 3k + 3 = 3(k + 1) chia hết cho 3 nên n(n + 1)(n + 2) chia hết cho 3.

Suy ra n(n + 1)(n + 2) chia hết cho 3 với mọi số nguyên n.

Vậy n(n + 1)(n + 2) chia hết cho 2 và 3 với mọi số nguyên n.

b)

+) Nếu n chẵn thì n chia hết cho 2 thì n + 2 chia hết cho 4 nên n(n + 1)(n + 2)(n + 3) chia hết cho 8.

Nếu n lẻ thì n + 1 chia hết cho 2 thì n + 3 chia hết cho 4 nên n(n + 1)(n + 2)(n +3) chia hết cho 8.

Suy ra n(n + 1)(n + 2)(n +3) chia hết cho 8 với mọi số nguyên n.

+) Nếu n chia hết cho 3 thì n(n + 1)(n + 2)(n + 3) chia hết cho 3.

Nếu n chia cho 3 dư 1 thì n có dạng n = 3k + 1. Khi đó n + 2 = 3k + 3 = 3(k+1) chia hết cho 3 nên n(n + 1)(n + 2)(n + 3) chia hết cho 3

Nếu n chia cho 3 dư 2 thì n có dạng n = 3k + 2. Khi đó n + 1 = 3k + 2 + 1 = 3k + 3 = 3(k + 1) chia hết cho 3 nên n(n + 1)(n + 2)(n + 3) chia hết cho 3.

Suy ra n(n + 1)(n + 2)(n + 3) chia hết cho 3 với mọi số nguyên n.

Vậy n(n + 1)(n + 2)(n + 3) chia hết cho 2 và 3 với mọi số nguyên n.

Bài 68 trang 88 sách bài tập Toán lớp 6 Tập 1:

a) Có tồn tại số tự nhiên n để n² + n + 2 chia hết cho 5 hay không?

b) Tìm số tự nhiên n nhỏ nhất sao cho n vừa là tổng của 5 số tự nhiên liên tiếp, vừa là tổng của 7 số tự nhiên liên tiếp.

Lời giải:

a) Đặt x = n² + n + 2

Nếu n chia hết cho 5 thì x chia 5 dư 2.

Nếu n chia cho 5 dư 1 thì x chia cho 5 dư 4.

Nếu n chia cho 5 dư 2 thì x chia cho 5 dư 3.

Nếu n chia cho 5 dư 3 thì x chia cho 5 dư 4.

Nếu n chia cho 5 dư 4 thì x chia cho 5 dư 2.

Vậy x không chia hết cho 5 với mọi số tự nhiên n.

b) Ta có n = a + (a + 1) + (a + 2) + (a + 3) + (a + 4) với a là số tự nhiên

Khi đó n = 5a + 10 = 5.(a + 2) chia hết cho 5.

Ta lại có n = b + (b + 1) + (b + 2) + (b + 3) + (b + 4) + (b + 5) + (b + 6) với b là số tự nhiên.

Khi đó n = 7b + 21 = 7.(b + 3) chia hết cho 7.

Do đó n vừa chia hết cho 5 vừa chia hết cho 7 nên n là bội chung của 5 và 7.

Mà n là nhỏ nhất nên n là BCNN(5; 7).

Ta có 5 = 5, 7 = 7.

BCNN(5, 7) = 5.7 = 35.

Vậy n = 35.

Bài 69 trang 88 sách bài tập Toán lớp 6 Tập 1: Tìm số nguyên x, biết:

a) 2x – 1 là bội của x – 3;

b) 2x + 1 là ước của 3x + 2;

c) (x – 4)(x + 2) + 6 không là bội của 9;

d) 9 không là ước của (x – 2)(x + 5) + 11

Lời giải:

a) Ta có 2x – 1 là bội của x – 3 nên 2x – 1 chia hết cho x – 3.

Ta lại có 2x – 1 = 2x – 6 + 5 = 2(x – 1) + 5.

Vì 2(x – 1) chia hết cho x – 1 nên 5 phải chia hết cho x – 1 hay x – 1 thuộc Ư(5) = {1; -1; 2; -2}.

Suy ra x thuộc {2; 0; 3; -1}.

Vậy x ∈ {2; 0; 3; -1}.

b) Ta có 2x + 1 là ước của 3x + 2 nên 3x + 2 chia hết cho 2x + 1

Suy ra: 2(3x + 2) = 6x + 4 = 3(2x + 1) + 1 cũng chia hết cho 2x + 1

Mà 3(2x + 1) chia hết cho 2x + 1 nên 1 cũng phải chia hết cho 2x + 1 hay 2x + 1 thuộc Ư(1) = {1; -1}.

Suy ra x thuộc {0; -1}.

Vậy x ∈ {0; -1}.

c)

+) Nếu x chia hết cho 3 thì x có dạng x = 3k với . Khi đó:

(x – 4)(x + 2) + 6 = (3k – 4)(3k + 2) + 6 không chia hết cho 3 nên không là bội của 9.

+) Nếu x chia cho 3 thì x có dạng x = 3k + 1 với . Khi đó:

(x – 4)(x + 2) + 6 = (3k – 3)(3k + 3) + 6 = 9(k – 1)(k + 3) + 6.

Vì 9(k – 1)(k + 3) chia hết cho 9 mà 6 không chia hết cho 9 nên 9(k – 1)(k + 3) + 6 không chia hết cho 9 hay (x – 4)(x + 2) + 6 không là bội của 9.

+) Nếu x chia cho 3 dư 2 thì x có dạng x = 3k + 2 với . Khi đó:

(x – 4)(x + 2) + 6 = (3k – 2)(3k + 4) + 6 không chia hết cho 3 nên không là bội của 9.

Vậy (x – 4)(x + 2) + 6 không là bội của 9 với mọi x nguyên.

d)

+) Nếu x chia hết cho 3 thì x có dạng x = 3k với . Khi đó:

(x – 2)(x + 5) + 11 = (3k – 2)(3k + 5) + 11 không chia hết cho 3 nên không là bội của 9.

+) Nếu x chia cho 3 thì x có dạng x = 3k + 1 với . Khi đó:

(x – 2)(x + 5) + 6 = (3k – 1)(3k + 6) + 6 = 3(3k – 1)(k + 2) + 11.

Vì 3(3k – 1)(k + 2) chia hết cho 3 mà 11 không chia hết cho 3 nên 3(3k – 1)(k + 2) + 11 không chia hết cho 3 nên không là bội của 9.

+) Nếu x chia cho 3 dư 2 thì x có dạng x = 3k + 2 với . Khi đó:

(x – 2)(x + 5) + 11 = (3k – 4)(3k + 7) + 11 không chia hết cho 3 nên không là bội của 9.

Vậy (x – 4)(x + 2) + 6 không là bội của 9 với mọi x nguyên.

Bài 70 trang 88 sách bài tập Toán lớp 6 Tập 1:

a) (2a – 1).(b² + 1) = -17;

b) (3 – a)(5 – b) = 2;

c) ab = 18, a + b = 11.

Lời giải:

a) Ta có (2a – 1).(b² + 1) = -17 nên b² + 1 là ước của 17 mà b² + 1  1 nên b² + 1 = 17 hoặc b² + 1 = 1.

Ta có bảng sau:

Vậy các cặp (a, b) thỏa mãn là: (0; -8), (4; 0), (-4; 0).

b) Ta có (3 – a)(5 – b) = 2 nên 3 – a là ước của 2 hay 3 – a  Ư(2) =

Vậy các cặp (a, b) thỏa mãn là: (2; 3), (1; 4), (4; 7), (5; 6).

c) ab = 18, a + b = 11.

Ta có ab = 18 nên a thuộc Ư(18) =

Khi đó ta có bảng sau:

Vậy các cặp (a, b) thỏa mãn là: (2; 9) và (9; 2).

Bài 71 trang 88 sách bài tập Toán lớp 6 Tập 1: Tìm số nguyên x, sao cho: 

a) A = x² + 2 021 đạt giá trị nhỏ nhất.

b) B = 2 022 – 20x²⁰ – 22x²² đạt giá trị lớn nhất.

Lời giải:

a) Vì với mọi giá trị nguyên của x nên .

Dấu “=” xảy ra khi x² = 0 hay x = 0.

Vậy A đạt giá trị nhỏ nhất 2 021 tại x = 0.

b) Vì với mọi giá trị nguyên của x nên với mọi giá trị nguyên của x.

Vì với mọi giá trị nguyên của x nên với mọi giá trị nguyên của x.

Do đó với mọi giá trị nguyên của x.

Suy ra với mọi giá trị nguyên của x.

Dấu “=” xảy ra khi x²² = 0 và x²⁰ = 0 hay x = 0.

Vậy B đạt giá trị lớn nhất bằng 2 022 khi x = 0.

Xem thêm các bài giải SBT Toán 6 Cánh diều hay, chi tiết khác:

Bài 5: Phép nhân các số nguyên

Bài 6: Phép chia hết hai số nguyên. Quan hệ chia hết trong tập hợp số nguyên

Bài 1: Tam giác đều. Hình vuông. Lục giác đều

Bài 2: Hình chữ nhật. Hình thoi

Bài 3: Hình bình hành