Sách bài tập Toán 6 Bài 1: Tam giác đều. Hình vuông. Lục giác đều
Lời giải:
Một số hình có dạng hình vuông trong thực tiễn là: viên gạch hoa, thảm, …


Một số hình có dạng hình lục giác đều trong thực tiễn là: khay để bánh kẹo, tổ ong, …


Bài 2 trang 105 sách bài tập Toán lớp 6 Tập 1: Trong các hình dưới đây, hình nào là tam giác đều?
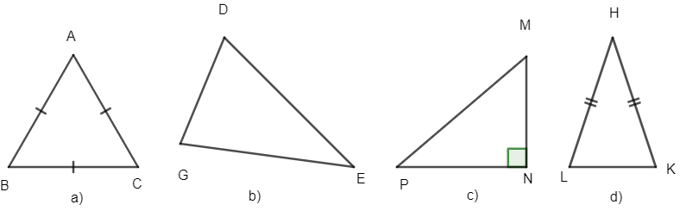
Lời giải:
Trong các hình trên, chỉ có hình a) là tam giác đều. Vì có ba cạnh bằng nhau (AB = AC = BC).
Bài 3 trang 105 106 sách bài tập Toán lớp 6 Tập 1: Các phát biểu sau đúng hay sai?
a) Nếu tam giác MNP là tam giác đều thì độ dài ba cạnh MN, NP, PM luôn bằng 2cm.
b) Tam giác đều ABC có ba cạnh bằng nhau và ba góc ở đỉnh A, B, C bằng nhau.
c) Nếu tam giác IKH có IK = IH và hai góc ở các đỉnh K, H bằng nhau thì tam giác IKH là tam giác đều.
Lời giải:
Phát biểu a) là phát biểu sai. Vì một tam giác đều khi có ba cạnh bằng nhau không nhất thiết phải bằng 2cm, có thể bằng 3cm, 4cm, …
Phát biểu b) là đúng. Vì tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.
Phát biểu c) là sai. Vì tam giác IKH chỉ có hai cạnh và hai góc bằng nhau nên chưa đủ điều kiện để tam giác IKH là tam giác đều.
Lời giải:
Bước 1. Vẽ cạnh MN = 5cm ( hoặc có thể chọn vẽ MP = 5cm hoặc NP = 5cm đều được).

Bước 2. Dùng compa vẽ các đường tròn tâm M bán kính 5cm và đường tròn tâm N bán kính 5cm.
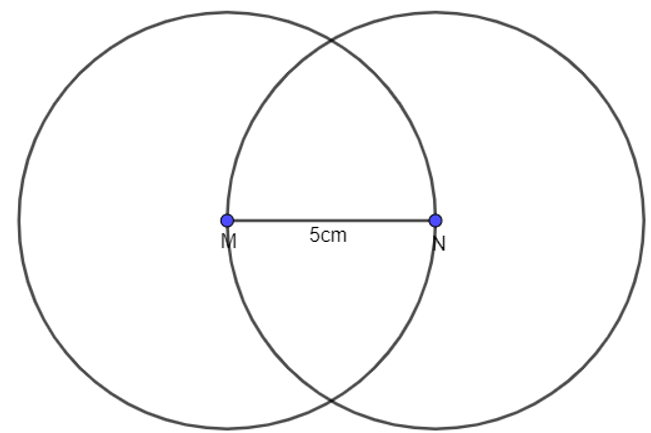
Bước 3. Hai đường tròn này giao nhau tại điểm P (vì hai đường tròn giao nhau tại hai điểm nên có thể tùy chọn đặt một trong hai giao điểm đó là điểm P). Nối M với P và N với P ta được tam giác đều MNP cạnh 5cm.
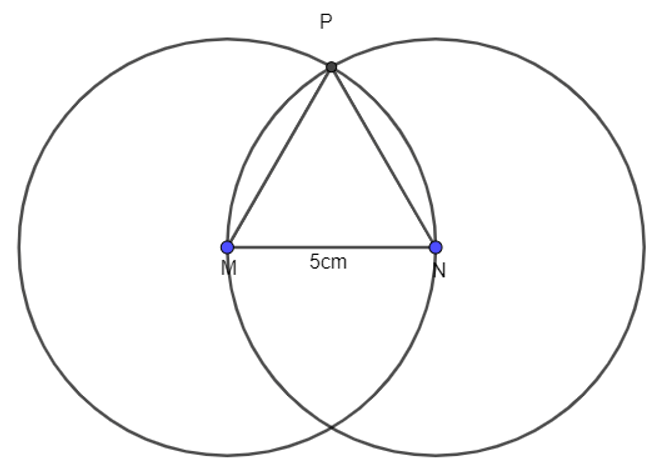
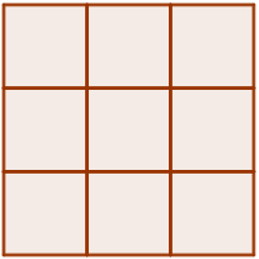
Bài 5 trang 106 sách bài tập Toán lớp 6 Tập 1: Mỗi hình sau có bao nhiêu ô vuông?
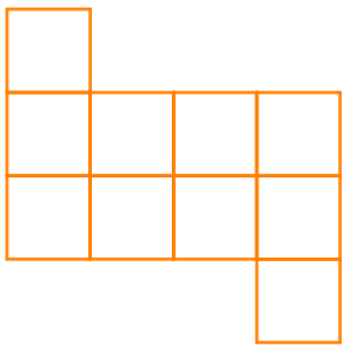
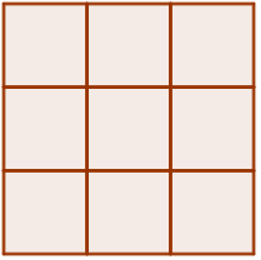
Hình a) Hình b)
Lời giải:
Đối với hình a) ta có:
+) 10 ô vuông nhỏ:
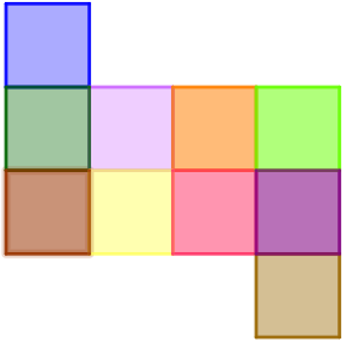
+) 3 ô vuông vừa:
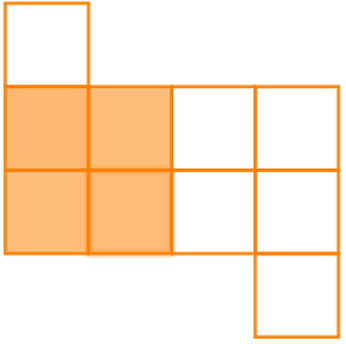
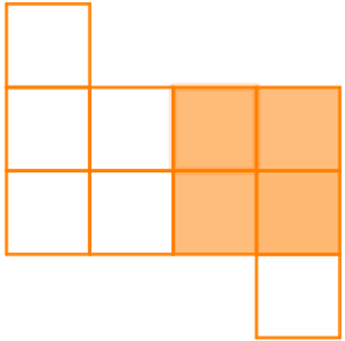
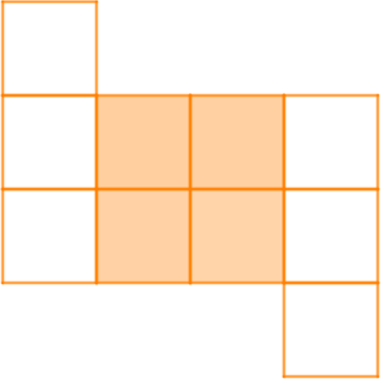
Vậy hình a) có tổng cộng 13 hình vuông.
Đối với hình b) ta có:
+) 9 ô vuông nhỏ:

+) Có 4 ô vuông vừa:
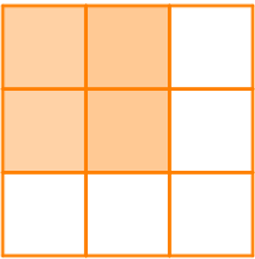
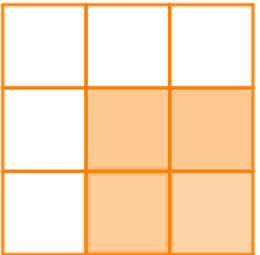
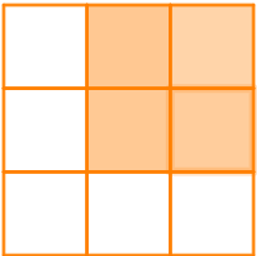
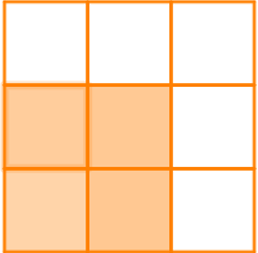
+) Và 1 hình vuông to ở bên ngoài
Vậy hình b) có tổng cộng 14 hình vuông.
Lời giải:
Đặt tên các đỉnh vào hình vẽ như sau:
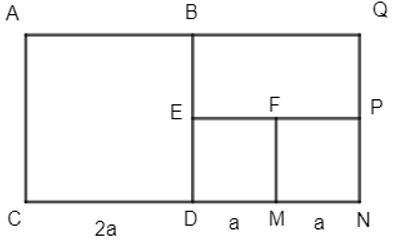
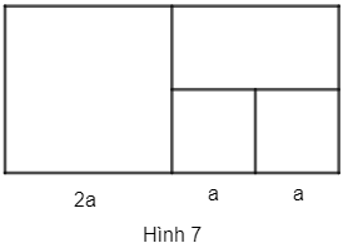
Ta có 4 hình vuông lần lượt là: ABCD, DEFM, MFPN, BQND.
Chu vi hình vuông ABCD bằng chu vi hình vuông BQND bằng: 2a.4 = 8a.
Chu vi hình vuông DEFM bằng chu vi hình vuông FPNM bằng: a.4 = 4a.
Tổng chu vi của bốn hình vuông là: 8a + 8a + 4a + 4a = 24a.
Mặt khác, tổng chu vi của cả bốn hình là 144cm nên ta có:
24a = 144 ⇒ a = 144:24 = 6 cm ⇒ 2a = 2.6 = 12cm.
Diện tích hình vuông ABCD bằng diện tích hình vuông BQDN bằng: 122 = 144 cm2.
Diện tích hình vuông DEFM bằng diện tích hình vuông FPNM bằng: 62 = 36 cm2.
Tổng diện tích của bốn hình vuông đó là: 144.2 + 36.2 = 360cm2.
Vậy tổng diện tích của bốn hình vuông là: 360cm2.
Lời giải:
Do diện tích hình vuông bằng bình phương độ dài cạnh của hình vuông đó và diện tích hình vuông là số tự nhiên có hai chữ số nên số đo diện tích có thể là:
42 = 16; 52 = 25; 62 = 36; 72 = 49; 82 = 64; 92 = 81.
Hơn nữa ta lại có chữ số hàng đơn vị của số đo diện tích hình vuông là 4 nên diện tích của miếng tôn là 64 dm2. Do đó cạnh miếng tôn có độ dài bằng 8dm.
Vậy độ dài cạnh của miếng tôn là 8dm.
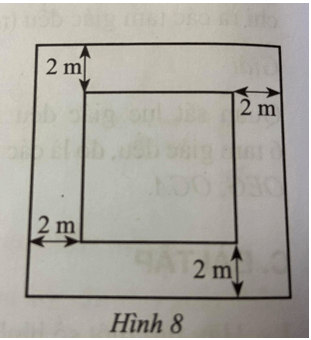
Lời giải:
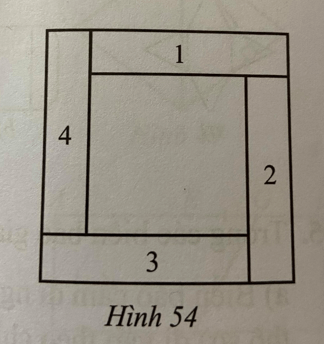
Diện tích phần mở rộng của khu vườn ta chia thành các phần 1, 2, 3 và 4 như hình vẽ trên.
Khi đó ta có: S1 + S2 + S3 + S4 = 80 m2.
Hơn nữa diện tích các phần này bằng nhau nên ta có: : S1 = S2 = S3 = S4 = 80:4 = 20 m2.
Sau khi mở rộng khu vườn thì cạnh của vườn trường là:
20:2 + 2 = 12 m.
Vậy cạnh của vườn trường sau khi mở rộng là 12m.
Bài 9 trang 106 sách bài tập Toán lớp 6 Tập 1: Vẽ hình theo mẫu ở Hình 9
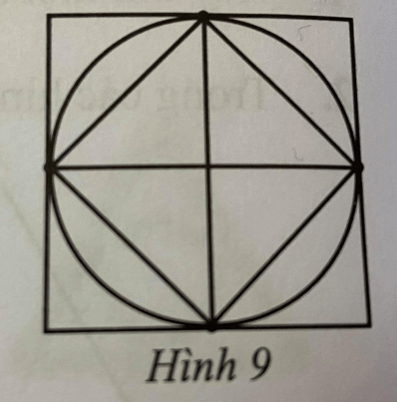
Lời giải:
Bước 1. Vẽ hình vuông ABCD cạnh 4cm (có thể tùy chỉnh số đo cạnh của hình vuông).
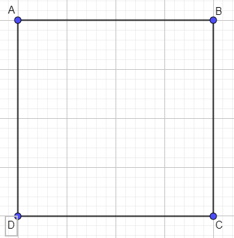
Bước 2. Kẻ AC, BD hai đường này giao nhau tại O.
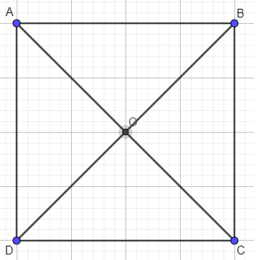
Bước 3. Vẽ đường tròn tâm O bán kính 2cm (bằng cạnh hình vuông ABCD chia đôi).
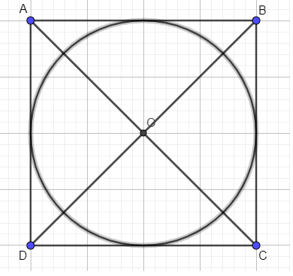
Bước 4. Đường tròn này tiếp xúc với các cạnh AB, BC, CD, AD của hình vuông ABCD lần lượt tại các điểm M, N, P, Q.
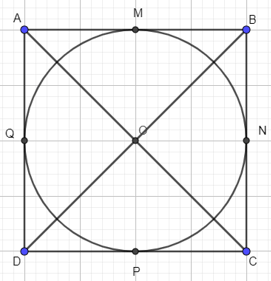
Bước 5. Nối M với N, N với P, P với Q, Q với M, M với P và N với Q và xóa hai đường chéo AC, BD ta được hình 9.
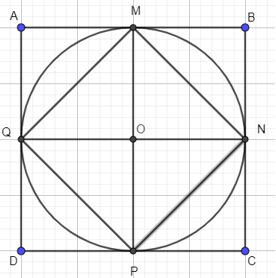
Lời giải:
Lục giác đều được ghép bởi sau tam giác đều.
Mà đường chéo chính của lục giác đều bằng 12cm nên độ dài cạnh lúc giác đều bằng một nửa đường chéo chính và bằng 6cm.
Chu vi của lục giác đều ABCDEG là: 6.6 = 36cm.
Vậy chu vi lục giác đều ABCDEG là 36cm.
Xem thêm các bài giải SBT Toán 6 Cánh diều hay, chi tiết khác:
Bài 6: Phép chia hết hai số nguyên. Quan hệ chia hết trong tập hợp số nguyên

