Giải Sách bài tập Toán 10 Bài tập cuối chương 1
Giải SBT Toán 10 trang 18 Tập 1
A. Trắc nghiệm
Bài 1 trang 18 SBT Toán 10 Tập 1: Mệnh đề nào sau đây đúng?
A. 0 = {0};
B. 0 ∈ {0};
C. 0 ⊂ {0};
D. 0 = ∅.
Lời giải:
Đáp án đúng là: B
Ta có {0} là một tập hợp, 0 là một phần tử nên viết 0 = {0} là sai, do đó đáp án A sai.
0 là một phần tử của tập hợp {0}, do đó ta viết 0 ∈ {0} là đúng nên đáp án B đúng.
Kí hiệu ⊂ dùng để chỉ mối quan hệ giữa các tập hợp nên đáp án C sai.
∅ là một tập hợp nên đáp án D sai.
Bài 2 trang 18 SBT Toán 10 Tập 1: Biết rằng P ⇒ Q là mệnh đề đúng. Mệnh đề nào sau đây đúng?
A. P là điều kiện cần để có Q;
B. P là điều kiện đủ để có Q;
C. Q là điều kiện cần và đủ để có P;
D. Q là điều kiện đủ để có P.
Lời giải:
Đáp án đúng là: B
Ta có P ⇒ Q là mệnh đề đúng, khi đó, ta có thể nói bằng một trong các cách sau:
+ P suy ra Q;
+ P kéo theo Q;
+ P là điều kiện đủ để có Q;
+ Q là điều kiện cần để có P.
Vậy trong các đáp án đã cho, đáp án B là đáp án đúng.
Bài 3 trang 18 SBT Toán 10 Tập 1: Cho số thực x. Mệnh đề nào sau đây là điều kiện đủ của “x > 1”?
A. x > 0;
B. x ≥ 1;
C. x < 1;
D. x ≥ 2.
Lời giải:
Đáp án đúng là: D
Ta có P ⇒ Q là mệnh đề đúng thì P là điều kiện đủ để có Q.
Xét các mệnh đề:
+ “Nếu x > 0 thì x > 1”, đây là mệnh đề sai, chẳng hạn ta có thể lấy x = 1, có 1 > 0 đúng nhưng 1 > 1 sai.
+ “Nếu x ≥ 1 thì x > 1”, đây là mệnh đề sai, chẳng hạn ta có thể lấy x = 1, có 1 ≥ 1 đúng nhưng 1 > 1 sai.
+ “Nếu x < 1 thì x > 1”, đây là mệnh đề sai.
+ “Nếu x ≥ 2 thì x > 1”, đây là mệnh đề đúng do 2 > 1.
Vậy mệnh đề “x ≥ 2” là điều kiện đủ của “x > 1”.
Bài 4 trang 18 SBT Toán 10 Tập 1: Mệnh đề nào sau đây sai?
(1) ∅ ∈ {0};
(2) {1} ⊂ {0; 1; 2};
(3) {0} = ∅;
(4) {0} ⊂ {x | x2 = x}.
A. (1) và (3);
B. (1) và (4);
C. (2) và (4);
D. (2) và (3).
Lời giải:
Đáp án đúng là: A
Ta có: ∅ và {0} đều là các tập hợp, mà kí hiệu ∈ dùng để chỉ mối quan hệ giữa phần tử và tập hợp nên mệnh đề (1) sai.
Tập hợp {1} gồm một phần tử là 1, phần tử này thuộc tập {0; 1; 2} nên {1} ⊂ {0; 1; 2}, do đó mệnh đề (2) đúng.
Tập ∅ không chứa phần tử nào, tập {0} chứa một phần tử 0, nên hai tập này không thể bằng nhau, do đó mệnh đề (3) sai.
Ta có: x2 = x ⇔ x = 0 hoặc x = 1, do đó {x | x2 = x} = {0; 1}.
Có {0} ⊂ {0; 1}, từ đó suy ra {0} ⊂ {x | x2 = x} nên mệnh đề (4) đúng.
Vậy trong các mệnh đề đã cho, mệnh đề (1) và (3) là mệnh đề sai.
A. 4;
B. 5;
C. 6;
D. 10.
Lời giải:
Đáp án đúng là: C
Do m và x là các số tự nhiên, nên ta lần lượt thay các giá trị của m bởi 0, 1, 2,... để tìm x thỏa mãn.
Ta có:
Với m = 0 thì x = 5 – 0 = 5 ∈ ℕ;
Với m = 1 thì x = 5 – 1 = 4 ∈ ℕ;
Với m = 2 thì x = 5 – 2 = 3 ∈ ℕ;
Với m = 3 thì x = 5 – 3 = 2 ∈ ℕ;
Với m = 4 thì x = 5 – 4 = 1 ∈ ℕ;
Với m = 5 thì x = 5 – 5 = 0 ∈ ℕ;
Với m = 6 thì x = 5 – 6 = – 1 ∉ ℕ, không thỏa mãn, ta dừng lại.
Vậy các giá trị x thỏa mãn là 0, 1, 2, 3, 4, 5.
Do đó, M = {0; 1; 2; 3; 4; 5} nên tập hợp M có 6 phần tử.
Bài 6 trang 18 SBT Toán 10 Tập 1: Tập hợp {y ∈ ℕ | y = 5 – x2, x ∈ ℕ} có bao nhiêu tập hợp con?
A. 3;
B. 4;
C. 8;
D. 16.
Lời giải:
Đáp án đúng là: C
Do y và x là các số tự nhiên, nên ta lần lượt thay các giá trị của x bởi 0, 1, 2,... để tìm y thỏa mãn.
Ta có:
Với x = 0 thì y = 5 – 02 = 5 ∈ ℕ;
Với x = 1 thì y = 5 – 12 = 4 ∈ ℕ;
Với x = 2 thì y = 5 – 22 = 1 ∈ ℕ;
Với x = 3 thì y = 5 – 32 = – 4 ∉ ℕ, không thỏa mãn, ta dừng lại.
Vậy các giá trị y thỏa mãn là 1, 4, 5.
Do đó, {y ∈ ℕ | y = 5 – x2, x ∈ ℕ} = {1; 4; 5}.
Các tập con của tập hợp {1; 4; 5} là ∅, {1}, {4}, {5}, {1; 4}, {1; 5}, {4; 5}, {1; 4; 5}.
Vậy có 8 tập con thỏa mãn.
Ngoài ra, ta có thể tính số tập con của một tập gồm k phần tử bằng cách tính 2k.
Tập {1; 4; 5} có 3 phần tử nên có 23 = 8 tập con.
A. {0; 1; 2};
B. {– 1};
C. {– 2; – 1};
D. {– 2}.
Lời giải:
Đáp án đúng là: A
Ta có: x + 1 ≤ 0 ⇔ x ≤ 0 – 1 ⇔ x ≤ – 1.
Do đó, B = {x | x + 1 ≤ 0} = {x | x ≤ – 1} = (– ∞; – 1].
Vậy A \ B = {– 2; – 1; 0; 1; 2} \ (– ∞; – 1] = {0; 1; 2}.
A. {2};
B. {– 1; 0; 1};
C. {1; 2};
D. {– 1; 0}.
Lời giải:
Đáp án đúng là: D
Ta có: x – 1 ≥ 0 ⇔ x ≥ 1.
Do đó, B = {x | x – 1 ≥ 0} = {x | x ≥ 1} = [1; + ∞).
Vậy A \ B = {– 1; 0; 1; 2} \ [1; + ∞) = {– 1; 0}.
A. B ∩ C = D;
B. C ∩ D = D;
C. B ∪ C = D;
D. B ∩ D = D.
Lời giải:
Đáp án đúng là: C
Lấy phần tử a tùy ý thuộc D, khi đó a là một hình vuông, mà hình vuông có 4 góc bằng nhau và bằng 90° nên nó cũng là hình chữ nhật, do đó a thuộc B.
Vậy D ⊂ B nên B ∩ D = D, đáp án D đúng.
Tương tự hình vuông thì có 4 cạnh bằng nhau nên nó cũng là một hình thoi, do đó a thuộc C. Vậy D ⊂ C nên C ∩ D = D, đáp án B đúng.
Hình thoi có 4 cạnh bằng nhau, hình chữ nhật có 4 góc bằng nhau và bằng 90°, do đó một hình vừa là hình chữ nhật vừa là hình thoi thì nó sẽ là hình vuông nên B ∩ C = D, đáp án A đúng.
Đáp án C sai do nếu ta có B ∪ C = D, x ∈ B ∪ C thì x ∈ D. Có x ∈ B ∪ C thì x là hình chữ nhật hoặc hình thoi, mà hình chữ nhật hoặc hình thoi thì chưa chắc đã là hình vuông nên vô lí.
A. a ≤ 1;
B. a < 1;
C. a ≥ 2;
D. a > 2
Lời giải:
Đáp án đúng là: B
Ta có: A = {x | x > a} = (a; + ∞).
B = {x | 1 < x < 2} = (1; 2).
Lại có CℝB = ℝ \ B = (– ∞; 1] ∪ [2; + ∞).
Để A ∪ (CℝB) = ℝ thì (a; + ∞) ∪ (– ∞; 1] ∪ [2; + ∞) = ℝ.
Từ đó suy ra a < 1.
Giải SBT Toán 10 trang 19 Tập 1
B. Tự luận
a) Nếu x ∈ A thì x ∈ C;
b) x ∈ A là điều kiện cần để x ∈ C;
c) x ∈ B là điều kiện đủ để x ∈ C;
d) Nếu x ∈ A thì x ∉ B;
e) x ∈ B là điều kiện đủ để x ∉ A.
Lời giải:
a) Vì A ⊂ C nên mọi phần tử của A đều là phần tử của C nên x ∈ A thì x ∈ C, mệnh đề a) đúng.
b) Mệnh đề “Nếu x ∈ A thì x ∈ C” là mệnh đề đúng (theo câu a), do đó, “x ∈ A là điều kiện đủ để x ∈ C”, vậy b) sai.
c) Vì B ⊂ C nên mọi phần tử của B đều là phần tử của C nên x ∈ B thì x ∈ C, ta có mệnh đề đúng là “Nếu x ∈ B thì x ∈ C” hay “x ∈ B là điều kiện đủ để x ∈ C”, do đó c) đúng.
d) Do A ∩ B = ∅, nên A và B là hai tập rời nhau hay mọi phần tử của A đều khác các phần tử trong B, khi đó ta có “Nếu x ∈ A thì x ∉ B” là mệnh đề đúng, vậy d) đúng.
e) Do A ∩ B = ∅, nên A và B là hai tập rời nhau hay mọi phần tử của A đều khác các phần tử trong B, khi đó ta có “Nếu x ∈ B thì x ∉ A” là mệnh đề đúng, do đó mệnh đề còn được phát biểu dưới dạng “x ∈ B là điều kiện đủ để x ∉ A”, vậy e) đúng.
Lời giải:
Ta có: A = {1; 2} và A ∪ B = {1; 2; 3}, mà 3 ∉ A, do đó 3 ∈ B, hơn nữa B ⊂ {1; 2; 3}.
Do đó, B là các tập con chứa phần tử 3 của tập {1; 2; 3}, đó là các tập: {3}, {1; 3}, {2; 3}, {1; 2; 3}.
Vậy các tập hợp B thỏa mãn yêu cầu là: {3}, {1; 3}, {2; 3}, {1; 2; 3}.
Lời giải:
Do M ∩ B = ∅ nên M và B là hai tập hợp rời nhau hay mọi phần tử của tập hợp M đều khác các phần tử trong tập hợp B, do đó tập hợp M không chứa các phần tử 3; 4; 5. (1)
Lại có M ⊂ A, do đó mọi phần tử của M đều là phần tử của A nên M có thể chứa các phần tử 1; 2; 3; 4. (2).
Từ (1) và (2) suy ra M chỉ có thể chứa các phần tử 1; 2.
Do đó, M = {1}, M = {2}, M = {1; 2}.
Lại có ∅ ⊂ A và ∅ ∩ B = ∅, do đó M = ∅.
Vậy các tập hợp M thỏa mãn là: ∅, {1}, {2}, {1; 2}.
a) Có bao nhiêu học sinh của thích cả hai môn trên?
b) Có bao nhiêu học sinh của thích bóng rổ nhưng không thích bóng bàn?
Lời giải:
Kí hiệu A là tập hợp các học sinh của lớp, B = {x ∈ A | x thích bóng rổ},
C = {x ∈ A | x thích bóng bàn}, D = {x ∈ A | x không thích môn nào trong hai môn}.
Theo giả thiết, ta có: n(A) = 36, n(B) = 20, n(C) = 14 và n(D) = 10.
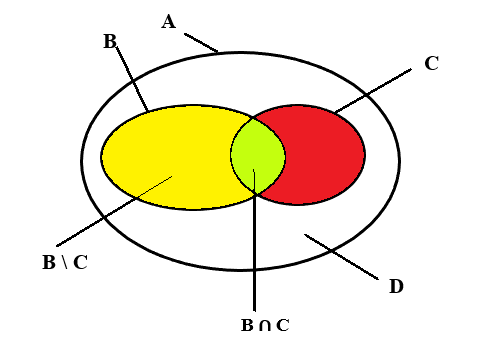
a) Số học sinh thích một trong hai môn là:
n(B ∪ C) = n(A) – n(D) = 36 – 10 = 26 (bạn).
Số học sinh thích cả hai môn thể thao trên là:
n(B ∩ C) = n(B) + n(C) – n(B ∪ C) = 20 + 14 – 26 = 8 (bạn).
b) Số học sinh thích bóng rổ nhưng không thích bóng bàn là:
n(B \ C) = n(B) – n(B ∩ C) = 20 – 8 = 12 (bạn).
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Các phép toán trên tập hợp
Bài 1: Bất phương trình bậc nhất hai ẩn




