Bài 4 trang 19 SBT Toán 10 Tập 1: Một học có 36 học sinh, trong đó 20 người thích bóng rổ, 14 người thích bóng bàn và 10 người không thích môn nào trong hai môn thể thao này.
a) Có bao nhiêu học sinh của thích cả hai môn trên?
b) Có bao nhiêu học sinh của thích bóng rổ nhưng không thích bóng bàn?
Kí hiệu A là tập hợp các học sinh của lớp, B = {x ∈ A | x thích bóng rổ},
C = {x ∈ A | x thích bóng bàn}, D = {x ∈ A | x không thích môn nào trong hai môn}.
Theo giả thiết, ta có: n(A) = 36, n(B) = 20, n(C) = 14 và n(D) = 10.
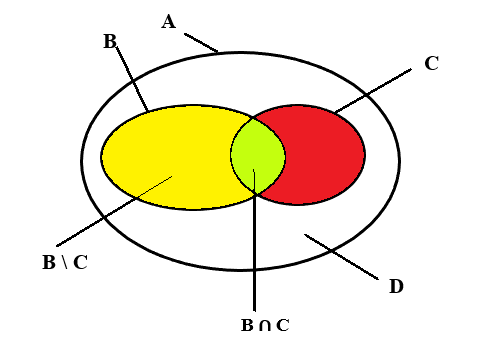
a) Số học sinh thích một trong hai môn là:
n(B ∪ C) = n(A) – n(D) = 36 – 10 = 26 (bạn).
Số học sinh thích cả hai môn thể thao trên là:
n(B ∩ C) = n(B) + n(C) – n(B ∪ C) = 20 + 14 – 26 = 8 (bạn).
b) Số học sinh thích bóng rổ nhưng không thích bóng bàn là:
n(B \ C) = n(B) – n(B ∩ C) = 20 – 8 = 12 (bạn).
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Các phép toán trên tập hợp
Bài 1: Bất phương trình bậc nhất hai ẩn