Giải Sách bài tập Toán 10 Bài 3: Các phép toán trên tập hợp
Giải SBT Toán 10 trang 16 Tập 1
Bài 1 trang 16 SBT Toán 10 Tập 1: Xác định A ∩ B, A ∪ B, A \ B, B \ A trong các trường hợp sau:
a) A = {a; b; c; d}, B = {a; c; e};
b) A = {x | x2 – 5x – 6 = 0}, B = {x | x2 = 1};
c) A = {x ∈ ℕ | x là số lẻ, x < 8}, B = {x ∈ ℕ | x là các ước của 12}.
Lời giải:
a) Ta có: A ∩ B = {x | x ∈ A và x ∈ B}
Các phần tử vừa thuộc A vừa thuộc B là: a; c.
Do đó A ∩ B = {a; c}.
Ta có: A ∪ B = {x | x ∈ A hoặc x ∈ B}
Các phần tử thuộc A hoặc thuộc B là: a; b; c; d; e.
Do đó A ∪ B = {a; b; c; d; e},
Ta có: A \ B = {x | x ∈ A và x ∉ B}
Các phần tử thuộc A nhưng không thuộc B là: b; d.
Do đó A \ B = {b; d}.
Ta có: B \ A = {x | x ∈ B và x ∉ A}
Phần tử thuộc B nhưng không thuộc A là: e.
Do đó, B \ A = {e}.
b) Giải phương trình x2 – 5x – 6 = 0.
Ta có: x2 – 5x – 6 = 0
⇔ x2 + x – 6x – 6 = 0
⇔ x(x + 1) – 6(x + 1) = 0
⇔ (x – 6)(x + 1) = 0
⇔ x = 6 hoặc x = – 1.
Do đó, A = {– 1; 6}.
Ta có: x2 = 1 ⇔ x = 1 hoặc x = – 1.
Do đó, B = {– 1; 1}.
Vậy A ∩ B = {x | x ∈ A và x ∈ B} = {– 1};
A ∪ B = {x | x ∈ A hoặc x ∈ B} = {– 1; 1; 6};
A \ B = {x | x ∈ A và x ∉ B} = {6};
B \ A = {x | x ∈ B và x ∉ A} = {1}.
c) Các số tự nhiên lẻ nhỏ hơn 8 là: 1; 3; 5; 7. Do đó, A = {1; 3; 5; 7}.
Các số tự nhiên là ước của 12 là: 1; 2; 3; 4; 6; 12. Do đó, B = {1; 2; 3; 4; 6; 12}.
Vậy A ∩ B = {x | x ∈ A và x ∈ B} = {1; 3};
A ∪ B = {x | x ∈ A hoặc x ∈ B} = {1; 2; 3; 4; 5; 6; 7; 12};
A \ B = {x | x ∈ A và x ∉ B} = {5; 7};
B \ A = {x | x ∈ B và x ∉ A} = {2; 4; 6; 12}.
Lời giải:
Ta thấy (x; y) ∈ A ∩ B khi (x; y) là nghiệm của hệ phương trình:(I){3x−2y=11 (1)2x+3y=3 (2).
Nhân hai vế của (1) với 3, nhân hai vế của (2) với 2, ta được hệ phương trình {9x−6y=334x+6y=6
Cộng vế với vế hai phương trình của hệ này, ta được 13x = 39 hay x = 3.
Thay x = 3 vào (1) ta được 3 . 3 – 2y = 11, suy ra y = – 1.
Do đó, hệ phương trình (I) có một nghiệm là (3; – 1).
Vậy A ∩ B = {(3; – 1)}.
a) (A ∪ B) ∩ C;
b) A ∩ (B ∩ C);
c) A \ (B ∩ C);
d) (A \ B) ∪ (A \ C).
Lời giải:
a) Ta có: A ∪ B = {x | x ∈ A hoặc x ∈ B} = {1; 2; 3; 4; 5; 7; 9}.
Do đó, (A ∪ B) ∩ C = {x | x ∈ (A ∪ B) và x ∈ C} = {3; 4; 5}.
b) Ta có: B ∩ C = {x | x ∈ B và x ∈ C} = {3; 4}.
Do đó, A ∩ (B ∩ C) = {x | x ∈ A và x ∈ (B ∩ C)} = {3}.
c) Ta có: A \ (B ∩ C) = {x | x ∈ A và x ∉ (B ∩ C)} = {1; 5; 7; 9}.
d) Ta có: A \ B = {x | x ∈ A và x ∉ B} = {5; 7; 9}.
A \ C = {x | x ∈ A và x ∉ C} = {1; 7; 9}.
Do đó, (A \ B) ∪ (A \ C) = {x | x ∈ (A \ B) hoặc x ∈ (A \ C)} = {1; 5; 7; 9}.
Giải SBT Toán 10 trang 17 Tập 1
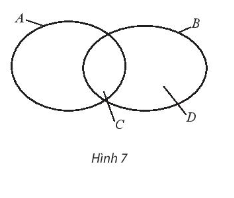
a) A ∩ B = ...;
b) C ∪ D = ...;
c) B \ A = ...;
d) B ∩ C = ...;
e) C \ A = ...;
g) D \ A = ...;
Lời giải:
a) Do A là tập hợp các học sinh nữ của trường và B là tập hợp các học sinh khối 10 của trường nên A ∩ B là tập hợp các học sinh nữ khối 10 của trường và chính là tập C.
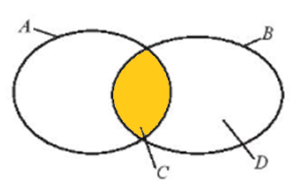
Do đó, A ∩ B = C.
b) Do C, D lần lượt là tập hợp các học sinh nữ, các học sinh nam khối 10 của trường nên C ∪ D là tập hợp các học sinh khối 10 của trường và chính là tập hợp B.
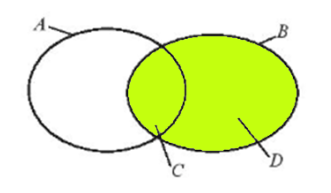
Do đó, C ∪ D = B.
c) B \ A là tập hợp các phần tử thuộc B nhưng không thuộc A, mà B là tập hợp các học sinh khối 10 của trường và A là tập hợp các học sinh nữ của trường, do đó B \ A là tập hợp các học sinh nam khối 10 của trường và chính là tập hợp D.
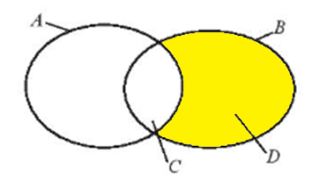
Vậy B \ A = D.
d) B ∩ C là tập hợp các phần tử vừa thuộc B vừa thuộc C, mà B là tập hợp các học sinh khối 10 của trường và C là tập hợp các học sinh nữ khối 10 của trường nên B ∩ C = C.
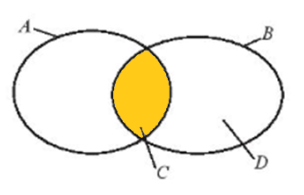
e) C \ A là tập hợp các phần tử thuộc C nhưng không thuộc A, theo sơ đồ Ven, ta thấy C ⊂ A. Do đó, C \ A = ∅.
g) D \ A là tập hợp các phần tử thuộc D nhưng không thuộc A, mà D là tập hợp các học sinh nam khối 10 của trường và A là tập hợp các học sinh nữ của trường, do đó D \ A là tập hợp các học sinh nam khối 10 của trường và chính là tập D.
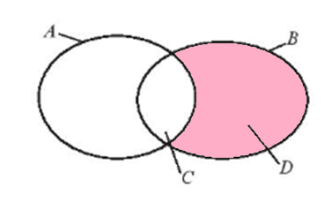
Vậy D \ A = D.
a) A ∩ A = ...;
b) A ∪ A = ...;
c) A ∩ ∅ = ...;
d) A ∪ ∅ = ...;
e) A \ A = ...;
g) A \ ∅ = ...;
h) ∅ \ A = ....
Lời giải:
a) A ∩ A = {x | x ∈ A và x ∈ A} = {x | x ∈ A} = A.
b) A ∪ A = {x | x ∈ A hoặc x ∈ A} = {x | x ∈ A} = A.
c) Do ∅ ⊂ A nên A ∩ ∅ = ∅.
d) Do ∅ ⊂ A nên A ∪ ∅ = A.
e) A \ A = {x | x ∈ A và x ∉ A} = ∅.
g) A \ ∅ = A. (Do tập ∅ không có chứa phần tử nào).
h) ∅ \ A = ∅.
a) Nếu B ⊂ A thì A ∩ B = ..., A ∪ B = ... và B \ A = ...;
b) Nếu A ∩ B = ∅ thì A \ B = ... và B \ A = ....
Lời giải:
a) Ta có B ⊂ A, ta biểu diễn sơ đồ Ven như sau:
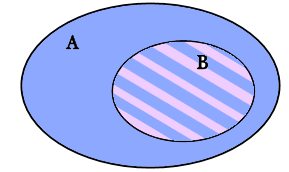
Khi đó, mọi phần tử của B đều là phần tử của A.
Vậy A ∩ B = B, A ∪ B = A và B \ A = ∅.
b) Ta có A ∩ B = ∅ nên A và B là hai tập hợp rời nhau:

Khi đó mọi phần tử của A và B đều khác nhau.
Vậy A \ B = A và B \ A = B.
Lời giải:
+ Để xác định A ∩ B ta vẽ sơ đồ sau:
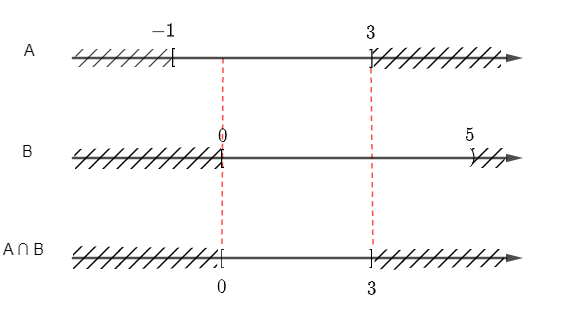
Từ sơ đồ, ta suy ra A ∩ B = [– 1; 3] ∩ [0; 5) = [0; 3].
+ Để xác định A ∪ B ta vẽ sơ đồ sau:
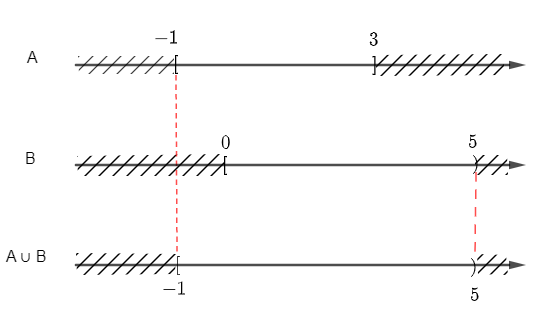
Từ sơ đồ, ta suy ra A ∪ B = [– 1; 3] ∪ [0; 5) = [– 1; 5).
+ Để xác định A \ B ta vẽ sơ đồ sau:
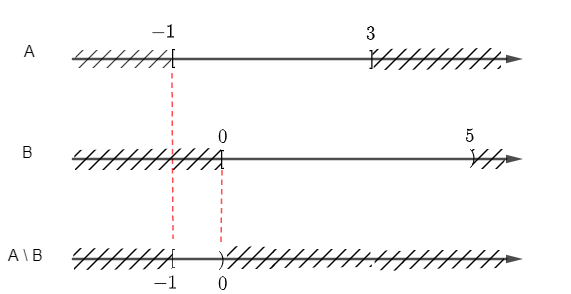
Từ sơ đồ, ta suy ra A \ B = [– 1; 3] \ [0; 5) = [– 1; 0).
+ Để xác định B \ A ta vẽ sơ đồ sau:
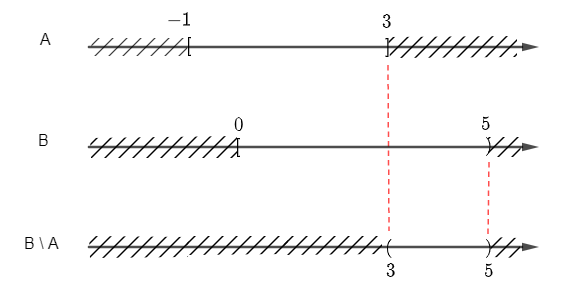
Từ sơ đồ, ta suy ra B \ A = [0; 5) \ [– 1; 3] = (3; 5).
a) 10E có bao nhiêu bạn chơi ít nhất một môn thể thao trên?
b) 10E có bao nhiêu học sinh?
Lời giải:
Kí hiệu A là tập hợp các học sinh của 10E, B = {x ∈ A | x chơi cầu lông},
C = {x ∈ A | x chơi cờ vua}, D = {x ∈ A |x không chơi cầu lông, cũng không chơi cờ vua}.
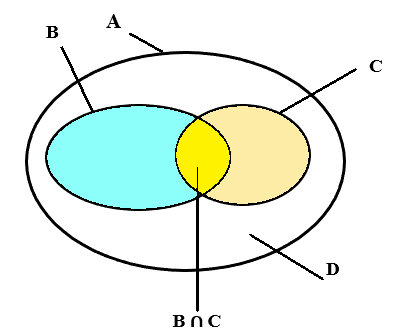
Theo giả thiết, n(B) = 18, n(C) = 15, n(B ∩ C) = 10 và n(D) = 12.
a) Số học sinh của 10E chơi ít nhất một môn thể thao là:
n(B ∪ C) = n(B) + n(C) – n(B ∩ C) = 18 + 15 – 10 = 23 (bạn).
b) Số học sinh của 10E là:
n(A) = n(B ∪ C) + n(D) = 23 + 12 = 35 (bạn).
Lời giải:
Do M ∩ {1; 3} = {1}, suy ra 1 ∈ M và 3 ∉ M.
Do M ∩ {5; 7} = {5}, suy ra 5 ∈ M và 7 ∉ M.
Do M ∩ {9; 11} = {9}, suy ra 9 ∈ M và 11 ∉ M.
Lại có M ⊂ {1; 3; 5; 7; 9; 11}.
Do đó, các phần tử của M là 1; 5; 9.
Vậy M = {1; 5; 9}.
Bài 10 trang 17 SBT Toán 10 Tập 1: Cho tập hợp A = {1; 2; 3},
a) tìm tất cả các tập hợp B sao cho A ∪ B = A;
b) tìm tất cả các tập hợp C sao cho A ∩ C = C.
Lời giải:
a) Ta có A ∪ B = A khi và chỉ khi mọi phần tử của B đều là phần tử của A hay B phải là tập con của A.
Mà A = {1; 2; 3}, nên các tập con của A là: ∅, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}.
Vậy các tập hợp B cần tìm là: ∅, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}.
b) Ta có A ∩ C = C khi và chỉ khi mọi phần tử của C đều là phần tử của A hay C là tập con của A.
Vậy các tập hợp C cần tìm là: ∅, {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}.
Lời giải:
Ta có: CUA = U \ A = {x | x ∈ U và x ∉ A}.
Mà CUA = {1}, do đó, 1 ∈ U = {3; 5; a2}, suy ra a2 = 1 nên a = 1 hoặc a = – 1.
+ Với a = 1, suy ra a + 4 = 1 + 4 = 5 nên ta có U = {1; 3; 5} và A = {3; 5}.
Khi đó, CUA = U \ A = {1} (thỏa mãn).
+ Với a = – 1, suy ra a + 4 = – 1 + 4 = 3 nên ta có U = {1; 3; 5} và A = {3}.
Khi đó, CUA = U \ A = {1; 5} (không thỏa mãn).
Vậy giá trị cần tìm là a = 1.
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:




