Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của F1F2, tia Ox
445
11/04/2023
HĐ2 trang 49 Toán 10 Tập 2: Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của F1F2, tia Ox trùng tia OF2 (H.7.21).
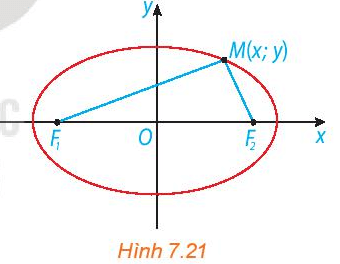
a) Nêu tọa độ của các tiêu điểm F1, F2.
b) Giải thích vì sao điểm M(x; y) thuộc elip khi và chỉ khi
√(x+c)2+y2+√(x−c)2+y2=2a. (1)
Chú ý. Người ta có thể biến đổi (1) về dạng x2a2+y2b2=1, với b=√a2−c2.
Trả lời
a) Vì F1F2 = 2c, mà O là trung điểm của F1F2.
Do đó ta có: F1O = F2O = 2c : 2 = c.
Quan sát hình ta thấy, điểm F1 thuộc trục Ox, nằm bên trái điểm O và cách O một khoảng bằng F1O nên tọa độ F1(– c; 0).
Điểm F2 thuộc trục Ox, nằm bên phải điểm O và cách O một khoảng bằng F2O nên tọa độ F2(c; 0).
Vậy tọa độ các tiêu điểm: F1(– c; 0) và F2(c; 0).
b) +) Giả sử M(x; y) thuộc elip (E) ta cần chứng minh: √(x+c)2+y2+√(x−c)2+y2=2a
Thật vậy, M thuộc elip (E) nên: MF1 + MF2 = 2a.
Lại có: MF1 = √(x−(−c))2+(y−0)2=√(x+c)2+y2 ;
MF2 = √(x−c)2+(y−0)2=√(x−c)2+y2.
⇒ MF1 + MF2 = √(x+c)2+y2+√(x−c)2+y2=2a.
Vậy √(x+c)2+y2+√(x−c)2+y2=2a.
+) Giả sử √(x+c)2+y2+√(x−c)2+y2=2a, ta cần chứng minh M thuộc elip (E).
Thật vậy: √(x+c)2+y2+√(x−c)2+y2=2a nên: MF1 + MF2 = 2a.
Vậy M thuộc elip (E).

