Hoạt động 6 trang 52 SGK Toán lớp 10 Tập 2: Xét (P) là một parabol với tiêu điểm F và đường chuẩn Δ

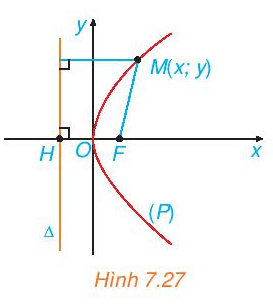
HĐ6 trang 52 Toán 10 Tập 2: Hoạt động 6 trang 52 SGK Toán lớp 10 Tập 2: Xét (P) là một parabol với tiêu điểm F và đường chuẩn Δ. Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên Δ. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của HF, tia Ox trùng tia OF (H.7.27). 

a) Nêu tọa độ của F và phương trình của ∆. 

b) Giải thích vì sao điểm M(x; y) thuộc (P) khi và chỉ khi 

$\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=\left|x+\frac{p}{2}\right|$. 

Trả lời

a) 

+) Khoảng cách từ F đến ∆, chính là FH và chính bằng tham số tiêu của (P) nên HF = p. 

Lại có O là trung điểm của HF nên HO = OF = $\frac{1}{2}HF=\frac{p}{2}$. 

Điểm F thuộc trục Ox và nằm bên phải điểm O và cách O một khoảng bằng OF nên tọa độ của F là F$\left(\frac{p}{2};0\right)$. 

Điểm H thuộc trục Ox và nằm bên trái điểm O và cách O một khoảng bằng OH nên tọa độ của H là H$\left(-\frac{p}{2};0\right)$. 

+) Đường thẳng ∆ đi qua điểm H$\left(-\frac{p}{2};0\right)$ và vuông góc với trục Ox, do đó phương trình của ∆ là x = $-\frac{P}{2}$ hay ∆: $x+\frac{p}{2}=0$. 

b) Ta có: MF = $\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}$.

d(M, ∆) = $\frac{\left|x+\frac{p}{2}\right|}{\sqrt{1^2+0}}=\left|x+\frac{p}{2}\right|$.

+) Giả sử M thuộc (P), ta cần chứng minh $\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=\left|x+\frac{p}{2}\right|$. 

Thật vậy, vì M thuộc (P) nên MF = d(M, ∆). 

$\iff \sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=\left|x+\frac{p}{2}\right|$. 

+) Giả sử $\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=\left|x+\frac{p}{2}\right|$, ta cần chứng minh M thuộc (P). 

Thật vậy, vì $\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=\left|x+\frac{p}{2}\right|$ nên MF = d(M, ∆). 

Vậy M thuộc (P).