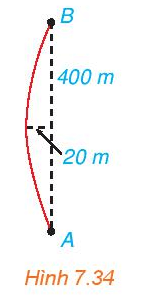
Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400 m

Bài 7.25 trang 56 Toán 10 Tập 2: Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400 m. Đỉnh parabol (P) của khúc của cách đường thẳng AB một khoảng 20 m và cách đều A, B (H.7.34).

a) Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế.

b) Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế.

Trả lời

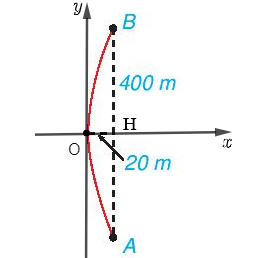
Chọn hệ trục tọa độ Oxy sao cho đỉnh của parabol trùng với gốc tọa độ O(0; 0) (như hình vẽ).

Gọi H là hình chiếu của O lên AB, khi đó ta chứng minh được H là trung điểm của AB nên HA = HB =  $\frac{1}{2}$AB. 

Khoảng cách từ khúc cua đến đường thẳng AB là OH.

a) Khoảng cách AB = 400 m. 

Ta có: HA = HB = 400 : 2 = 200 (m).

OH = 20 m. 

Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế thì tọa độ các điểm là: A(20; – 200) và B(20; 200). 

Gọi phương trình parabol (P) có dạng y² = 2px (với p > 0). 

Khi đó A, B đều thuộc (P). 

Thay tọa độ điểm B vào phương trình parabol (P) ta có: 200² = 2p . 20 ⇔ 2p = 2000. 

Vậy parabol (P) có phương trình là: y² = 2000x. 

b) Đổi: 400 m = 0,4 km; 20 m = 0,02 km.

Khi đó HA = HB = 0,4 : 2 = 0,2 (km). 

OH = 0,02 km. 

Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế thì tọa độ các điểm là: A(0,02; – 0,2) và B(0,02; 0,2) 

Gọi phương trình parabol (P) có dạng y² = 2p'x (với p' > 0). 

Khi đó A, B đều thuộc (P). 

Thay tọa độ điểm B vào phương trình parabol (P) ta có: 0,2² = 2p' . 0,02 ⇔ 2p' = 2.

Vậy parabol (P) có phương trình là: y² = 2x.