Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh

Bài 34 trang 57 SBT Toán 10 Tập 1: Xét hệ tọa độ Oth trong mặt phẳng, trong đó trục Ot biểu thị thời gian t (tính bằng giây) và trục Oh biểu thị độ cao h (tính bằng mét). Một quả bóng được đá lên từ điểm A(0; 0,3) và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 8m sau 1 giây và đạt độ cao 6m sau 2 giây. Trong khoảng thời gian nào (tính bằng giây) thì quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m (làm tròn kết quả đến hàng phần nghìn).

Trả lời

Ta có hình vẽ mô phỏng quỹ đạo chuyển động của quả bóng như hình vẽ:

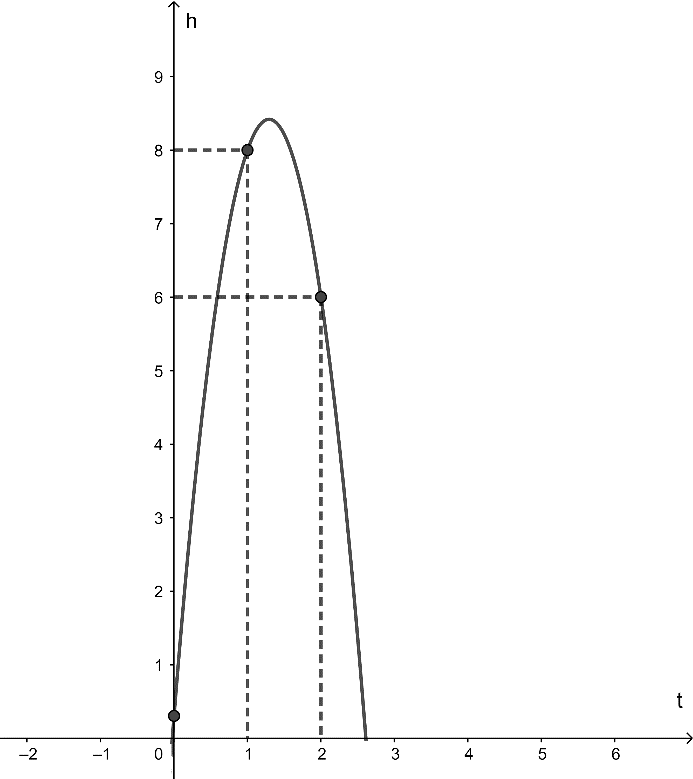
Vì quỹ đạo chuyển động là một đường thẳng parabol có dạng h = at² + bt + c (a ≠ 0).

Một quả bóng được đá lên từ điểm A(0; 0,3) nên điểm A thuộc vào parabol, thay t = 0 và h = 0,3 vào đồ thị hàm số ta được: 0,3 = a.0² + b.0 + c ⇔ c = 0,3 (1).

Bóng đạt độ cao h = 8m sau t = 1 giây nên điểm có tọa độ (1; 8) thuộc vào parabol.

Thay t = 1 và h = 8 vào đồ thị hàm số ta được: 8 = a.1² + b.1 + c ⇔ a + b + c = 8 (2).

Bóng đạt độ cao h = 6m sau t = 2 giây nên điểm có tọa độ (2; 6) thuộc vào parabol.

Thay t = 2 và h = 6 vào đồ thị hàm số ta được: 6 = a.2² + b.2 + c ⇔ 4a + 2b + c = 6 (3).

Từ (1), (2) và (3) ta có hệ phương trình: $\left\{\begin{array}{l}c=0,3\\ a+b+c=8\\ 4a+2b+c=6\end{array}\right.\iff \left\{\begin{array}{l}c=0,3\\ a=-4,85\\ b=12,55\end{array}\right.$.

Ta có phương trình parabol cần tìm là: h = – 4,85t² + 12,55t + 0,3.

Để chiều cao lớn hơn 5 thì h > 5 ⇔ – 4,85t² + 12,55t + 0,3 > 5

⇔ – 4,85t² + 12,55t – 4,7 > 0

Xét tam thức bậc hai f(t) = – 4,85t² + 12,55t – 4,7, có a = – 4,85, ∆ = 12,55² – 4.(– 4,85).(– 4,7) = 66,3225 > 0.

Suy ra tam thức có hai nghiệm phân biệt t₁ ≈ 0,454 và t₂ ≈ 2,133.

Áp dụng định lí về dấu của tam thức bậc hai ta được: f(t) > 0 hay – 4,85t² + 12,55t – 4,7 > 0 khi t ∈ (0,454; 2,133).

Để chiều cao nhỏ hơn 7 thì h < 7 ⇔ – 4,85t² + 12,55t + 0,3 < 7

⇔ – 4,85t² + 12,55t – 6,7 < 0

Xét tam thức bậc hai g(t) = – 4,85t² + 12,55t – 6,7, có a = – 4,85, ∆ = 12,55² – 4.(– 4,85).(– 6,7) = 27,5225 > 0.

Suy ra tam thức có hai nghiệm phân biệt t₁ ≈ 0,753 và t₂ ≈ 1,835.

Áp dụng định lí về dấu của tam thức bậc hai ta được: g(t) < 0 hay – 4,85t² + 12,55t – 6,7 < 0 khi t ∈ (– ∞; 0,753) ∪ (1,835; +∞).

Để quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m thì t phải thuộc vào giao của hai tập (0,454; 2,133) hoặc (– ∞; 0,753) ∪ (1,835; +∞).

Ta có (0,454; 2,133)  (– ∞; 0,753) ∪ (1,835; +∞) = (0,454; 0,753) ∪ (1,835; 2,133).

Vậy để quả bóng ở độ cao lớn hơn 5m và nhỏ hơn 7m thì thuộc khoảng 0,454 giây đến 0,753 giây hoặc 1,835 giây đến 2,133 giây.

Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Bài 4: Bất phương trình bậc nhất một ẩn

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Bài ôn tập chương 3

Bài 1: Định lí côsin và định lí sin trong tam giác. Giá trị lượng giác của một góc từ 0° đến 180°