Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi Hình 12a, 12b
Bài 18 trang 48 SBT Toán 10 Tập 1: Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi Hình 12a, 12b:
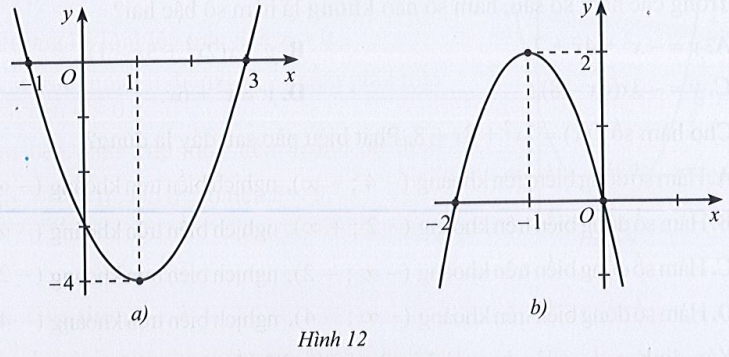
Bài 18 trang 48 SBT Toán 10 Tập 1: Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi Hình 12a, 12b:

+) Hình 12a):
Dựa vào hình vẽ, ta thấy:
- Đồ thị hàm số cắt trục tung tại điểm có tung độ – 3 nên c = – 3.
- Điểm đỉnh của parabol có tọa độ (1; – 4) nên ta có:
−b2a=1 ⇔ b = – 2a
−Δ4a=−4⇔ ∆ = 16a
⇔ b2 – 4ac = 16a
⇔ (– 2a)2 – 4a(– 3) = 16a
⇔ 4a2 + 12a = 16a
⇔ 4a2 – 4a = 0
⇔ 4a(a – 1) = 0
⇔ a = 0 (không thỏa mãn) hoặc a = 1 (thỏa mãn)
⇒ b = – 2a = – 2.1 = – 2.
Vậy hàm số bậc hai cần tìm là y = x2 – 2x – 3.
+) Hình 12b):
Dựa vào hình vẽ, ta thấy:
- Đồ thị hàm số cắt trục tung tại điểm có tung độ 0 nên c = 0.
- Điểm đỉnh của parabol có tọa độ (– 1; 2) nên ta có:
−b2a=−1 ⇔ b = 2a
−Δ4a=2⇔ ∆ = – 8a
⇔ b2 – 4ac = – 8a
⇔ (2a)2 – 4a.0 = – 8a
⇔ 4a2 = – 8a
⇔ 4a2 + 8a = 0
⇔ 4a(a + 2) = 0
⇔ a = 0 (không thỏa mãn) hoặc a = – 2 (thỏa mãn)
⇒ b = 2a = 2.(– 2) = – 4.
Vậy hàm số bậc hai cần tìm là y = – 2x2 – 4x.
Xem thêm lời giải sách bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Bài 3: Dấu của tam thức bậc hai