Với tất cả các giá trị thực nào của tham số m thì hàm số y = x³ − 3(m + 1)x² + 3m(m + 2)x nghịch biến trên đoạn [0; 1]?

Xét hàm số: y = x³ − 3(m + 1)x² + 3m(m + 2)x

Ta có: y¢ = 3x² − 6(m + 1)x + 3m(m + 2)

= 3x² − 3(m + 2)x − 3mx + 3m(m + 2)

= 3x(x − m − 2) − 3m(x − m − 2)

= 3(x − m − 2)(x − m)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = m\\x = m + 2\end{array} \right.\;\left( {m < m + 2,\;\forall m} \right)\)

Bảng biến thiên:

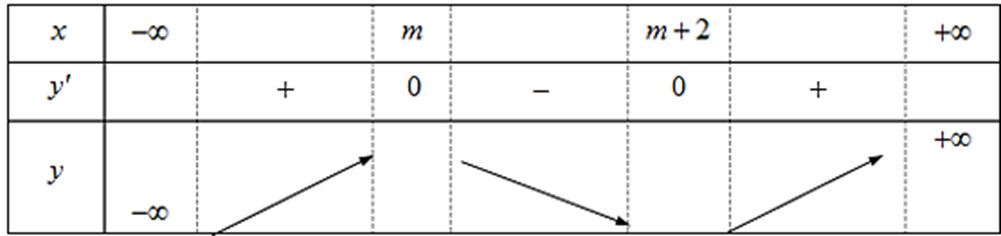
Theo bảng biến thiên, hàm số nghịch biến trên đoạn [0; 1] khi và chỉ khi:

y¢ ≤ 0, "x Î [0; 1]

\( \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m + 2 \ge 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge - 1\end{array} \right. \Leftrightarrow - 1 \le m \le 0\)

Vậy −1 ≤ m ≤ 0 là các giá trị của tham số m thỏa mãn.