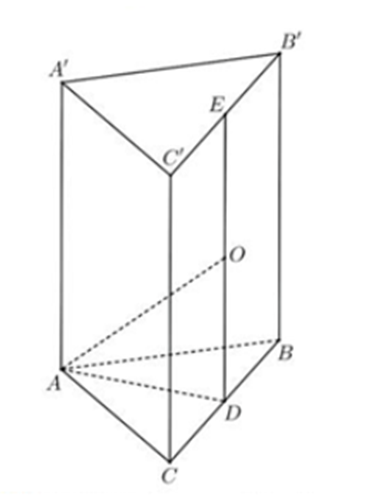
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, AB = AC = a và \[{\rm{AA}}' = a\sqrt 2 \]. Thể tích khối cầu ngoại tiếp hình tứ diện AB’A’C là:
A. \[\frac{{\pi {a^3}}}{3}\]
B. \(\pi {a^3}\)
C. \[\frac{{4\pi {a^3}}}{3}\]
D. \(4\pi {a^3}\).
Đáp án đúng là: C
Khối cầu ngoại tiếp hình tứ diện AB’A’C là khối cầu ngoại tiếp lăng trụ BAC.A’B’C’
Gọi D, E lần lượt là trung điểm của BC và B’C’, O là trung điểm của DE
Suy ra O là tâm khối cầu ngoại tiếp lăng trụ BAC.A’B’C’ (do đáy là ∆ABC vuông cân tại A)
Ta có: \(OD = \frac{{AA'}}{2} = \frac{{a\sqrt 2 }}{2}\)
Vì tam giác ABC vuông tại A nên \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {2{a^2}} = a\sqrt 2 \)
Suy ra \(AD = \frac{{BC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Do đó bán kính khối cầu ngoại tiếp lăng trụ ABC.A’B’C’ là
\(R = OA = \sqrt {A{D^2} + O{D^2}} = \sqrt {{a^2}} = a\)
Thể tích khối cầu cần tính là \(V = \frac{4}{3}\pi {R^3} = \frac{{4\pi {a^3}}}{3}\)
Vậy ta chọn đáp án C.