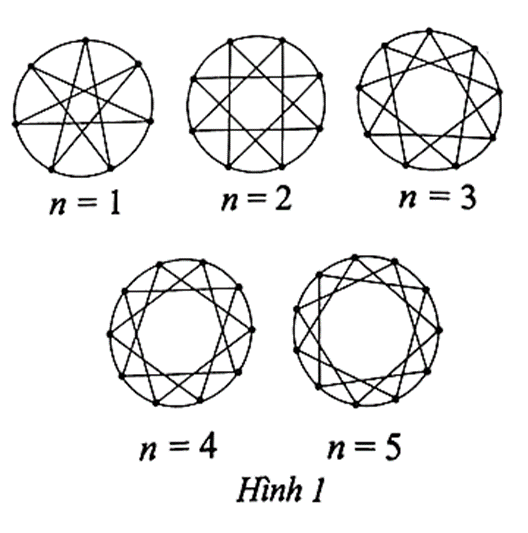
Với mỗi số nguyên dương n, lấy n + 6 điểm cách đều nhau trên đường tròn. Nối mỗi điểm với điểm cách nó hai điểm trên đường tròn đó để tạo thành các ngôi sao như Hình 1. Gọi u_n là số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao thì ta được dãy số (u_n). Tìm công thức của số hạng tổng quát u_n.

Ta thấy đường tròn được chia thành n + 6 cung bằng nhau và mỗi cung có số đo bằng \(\left( {\frac{{360}}{{n + 6}}} \right)\begin{array}{*{20}{c}}^\circ \\{}\end{array}\). Do mỗi điểm được nối với điểm cách nó hai điểm trên đường tròn nên góc ở đỉnh của mỗi ngôi sao là góc nội tiếp chắn n + 6 – 2 . 3 = n cung bằng nhau đó. Suy ra số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao là \({u_n} = \frac{1}{2}.\frac{{360}}{{n + 6}}.n = \frac{{180n}}{{n + 6}}\).