Từ đồ thị hàm số y = sin x, tìm: a) Các giá trị của x để sin x = 1/2
Từ đồ thị hàm số y = sin x, tìm:
Các giá trị của x để sin x = \(\frac{1}{2}\);
Xét đồ thị hàm số y = sin x và đường thẳng y = \(\frac{1}{2}\).
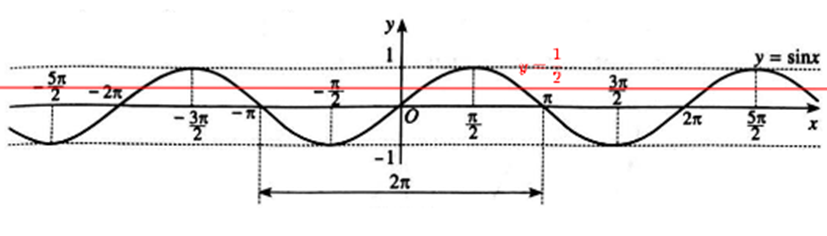
Giá trị của x để sin x = \(\frac{1}{2}\) là hoành độ giao điểm của đồ thị hàm số y = sin x và đường thẳng y = \(\frac{1}{2}\).
Dựa vào đồ thị, ta có sin x = \(\frac{1}{2}\) khi \(x = \frac{\pi }{6} + k2\pi \) và \(x = \frac{{5\pi }}{6} + k2\pi \) với k ∈ ℤ.