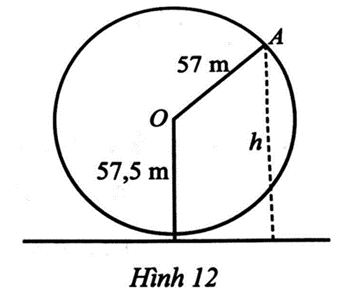
Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

\(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?

Khi t = 0 thì \(h\left( 0 \right) = 57\sin \left( {\frac{{2\pi }}{{15}}.0 - \frac{\pi }{2}} \right) + 57,5 = 57\sin \left( { - \frac{\pi }{2}} \right) + 57,5 = 0,5\) (m).

Vậy khi đó khoảng cách từ cabin đến mặt đất bằng 0,5 m.