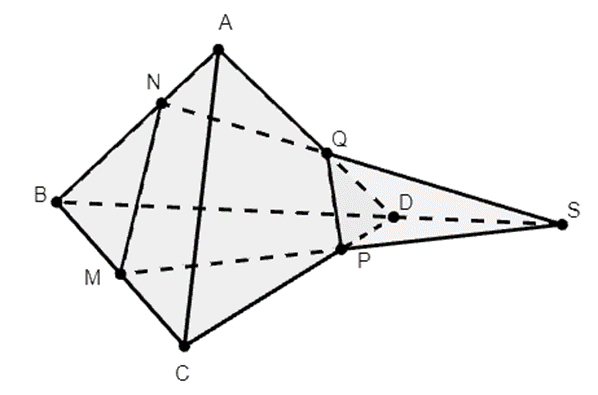
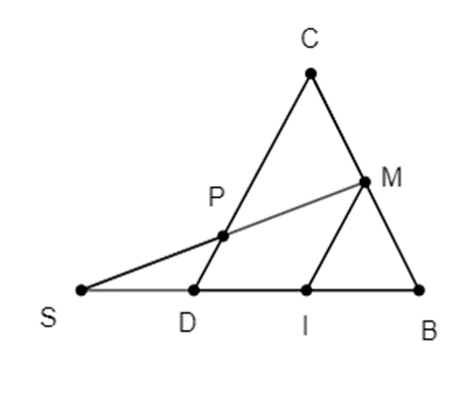
Tứ diện ABCD. Gọi M là trung điểm của BC. N là điểm nằm trên đoạn thẳng AB sao cho NB = 2NA, P là điểm nằm trên đoạn thẳng CD sao cho PC = 3PD, S là giao điểm của BD và MP, Q là giao điểm của SN và AD. Tính tỉ số \(\frac{{QD}}{{QA}}\).
Gọi I là trung điểm của BD.
Khi đó IM là đường trung bình của tam giác BCD nên IM // CD, \(IM = \frac{1}{2}CD\)
Mà \(PD = \frac{1}{4}CD \Rightarrow PD = \frac{1}{2}IM\)
⇒ PD là đường trung bình của tam giác SIM
⇒ D là trung điểm của SI
\( \Rightarrow BI = ID = SD \Rightarrow SD = \frac{1}{3}SB\)
Xét tam giác SAB có:\(\frac{{AN}}{{AB}} = \frac{{SD}}{{SB}} = \frac{1}{3}\).
Do đó ND // SA và \(\frac{{ND}}{{SA}} = \frac{{NB}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{QD}}{{QA}} = \frac{{ND}}{{SA}} = \frac{2}{3}\).