Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,5
Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là 0,5 mm, màn quan sát cách mặt phẳng chứa hai khe một khoảng 1,5 m. Chiếu sáng hai khe bằng ánh sáng tổng hợp gồm hai bức xạ có bước sóng
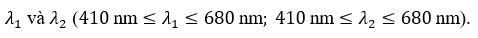
Trên màn quan sát người ta đánh dấu một điểm M cách vân sáng trung tâm một khoảng 12,6 mm. Tại M có vân sáng của bức xạ bước sóng 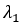 và vân tối của bức xạ bước sóng
và vân tối của bức xạ bước sóng 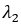 . Giữa M và vân sáng trung tâm có hai vị trí mà tại đó vân sáng của hai bức xạ trùng nhau. Để tại M chỉ có vân sáng của một bức xạ
. Giữa M và vân sáng trung tâm có hai vị trí mà tại đó vân sáng của hai bức xạ trùng nhau. Để tại M chỉ có vân sáng của một bức xạ 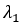 , phải dịch chuyển màn tịnh tiến theo phương vuông góc với màn, ra xa nguồn sáng thêm một khoảng nhỏ nhất bằng 16m . Bước sóng của hai bức xạ
, phải dịch chuyển màn tịnh tiến theo phương vuông góc với màn, ra xa nguồn sáng thêm một khoảng nhỏ nhất bằng 16m . Bước sóng của hai bức xạ 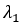 và
và 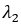 chênh lệch nhau
chênh lệch nhau
