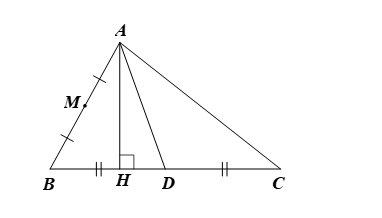
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có M(2; 0) là trung điểm của cạnh AB. Đường trung tuyến và đường

C. 3x – 4y + 5 = 0;

Trả lời

Hướng dẫn giải:

Đáp án đúng là: C

⦁ Gọi AH và AD lần lượt là các đường cao và trung tuyến kẻ từ A của tam giác ABC.

Tọa độ điểm A là nghiệm của hệ phương trình:

$\left\{\begin{array}{l}7x-2y-3=0\\ 6x-y-4=0\end{array}\right.\iff \left\{\begin{array}{l}x=1\\ y=2\end{array}\right..$ Do đó A(1; 2).

Vì M là trung điểm của AB nên: $\left\{\begin{array}{l}{x}_B=2x_M-x_A=3\\ y_B=2y_M-y_A=-2\end{array}\right..$ Do đó B(3; –2).

⦁ Ta có AH ⊥ BC nên vectơ chỉ phương của AH là vectơ pháp tuyến của BC.

Đường thẳng AH: 6x – y – 4 = 0 có ${\overrightarrow{n}}_{AH}=\left(6;-1\right)$ nên ${\overrightarrow{n}}_{BC}=\left(1;6\right).$

Đường thẳng BC đi qua B(3; –2) và nhận ${\overrightarrow{n}}_{BC}=\left(1;6\right)$ làm một vectơ pháp tuyến nên có phương trình là: 1(x – 3) + 6(y + 2) = 0 hay x + 6y + 9 = 0.

⦁ D là giao điểm của BC và AD nên tọa độ điểm D là nghiệm của hệ phương trình:

$\left\{\begin{array}{l}7x-2y-3=0\\ x+6y+9=0\end{array}\right.\iff \left\{\begin{array}{l}x=0\\ y=-\frac{3}{2}\end{array}\right..$ Do đó $D\left(0;-\frac{3}{2}\right).$

Mà D là trung điểm của BC nên suy ra: $\left\{\begin{array}{l}{x}_C=2x_D-x_B=-3\\ y_C=2y_D-y_B=-1\end{array}\right..$ Do đó C(–3; –1).

⦁ Với A(1; 2) và C(–3; –1) ta có $\overrightarrow{AC}=\left(-4;-3\right),$ suy ra ${\overrightarrow{n}}_{AC}=\left(3;-4\right).$

Đường thẳng AC đi qua A(1; 2) và nhận ${\overrightarrow{n}}_{AC}=\left(3;-4\right)$ làm một vectơ pháp tuyến nên có phương trình là: 3(x – 1) – 4(y – 2) = 0 tức là 3x – 4y + 5 = 0.