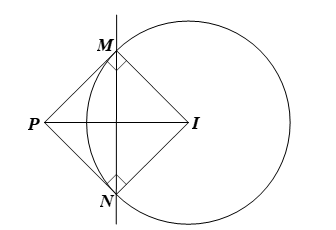
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)2 + (y – 4)2 = 36 và điểm P(–3; –2) nằm ngoài đường tròn.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)2 + (y – 4)2 = 36 và điểm P(–3; –2) nằm ngoài đường tròn. Từ điểm P kẻ các tiếp tuyến PM và PN tới đường tròn (C), với M, N là các tiếp điểm. Phương trình đường thẳng MN là
A. x + y + 1 = 0;
B. x – y – 1 = 0;
C. x – y + 1 = 0;