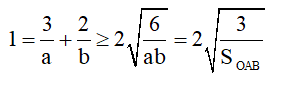Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua điểm M(3; 2), cắt tia Ox tại A và cắt tia Oy tại
26
16/11/2024
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d đi qua điểm M(3; 2), cắt tia Ox tại A và cắt tia Oy tại B sao cho diện tích tam giác OAB đạt giá trị nhỏ nhất. Khi đó phương trình đường thẳng d theo đoạn chắn là:
C. x32+y1=1;
D. x1+y32=1.
Trả lời
Hướng dẫn giải
Đáp án đúng là: B
Gọi A(a; 0) và B(0; b) (với a > 0, b > 0).
Khi đó phương trình đoạn chắn của d có dạng: xa+yb=1.
Đường thẳng d đi qua điểm M(3; 2) nên ta có 3a+2b=1.
Ta có diện tích tam giác OAB là: S=12OA⋅OB=12|a|⋅|b|=12ab.
Áp dụng BĐT Cauchy, ta được
Suy ra SOAB ≥ 12.
Dấu “=” xảy ra khi và chỉ khi 3a=2b=12⇔{a=6b=4.
Vậy đường thẳng d có phương trình theo đoạn chắn là x6+y4=1.