Trong mặt phẳng tọa độ Oxy, cho các điểm A(0; 6), B(6; 3) và điểm M thuộc trục hoành. a) Xác định điểm C

Bài 14 trang 25 Chuyên đề Toán 11: Trong mặt phẳng tọa độ Oxy, cho các điểm A(0; 6), B(6; 3) và điểm M thuộc trục hoành.

a) Xác định điểm C đối xứng với B qua trục hoành.

b) Chứng minh rằng MB = MC.

c) Xác định điểm M sao cho tổng MA + MB đạt giá trị nhỏ nhất.

Trả lời

a) Điểm B(6; 3) đối xứng với điểm C qua trục hoành Ox nên C là ảnh của B qua phép đối xứng trục Ox. Do đó C(6; – 3).

b) Vì C là ảnh của điểm B qua phép đối xứng trục Ox nên Ox là đường trung trực của đoạn thẳng BC, do đó điểm M thuộc đường trung trực Ox của BC thì M cách đều B và C, suy ra MB = MC.

c)

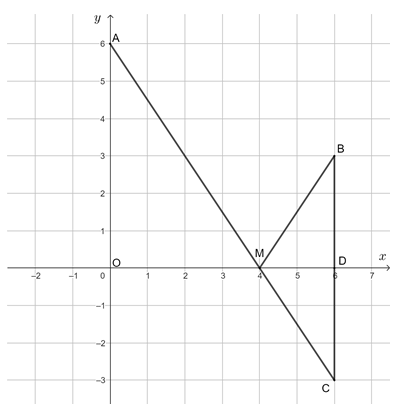
Vì MB = MC nên MA + MB = MA + MC.

Do A và C nằm khác phía nhau đối với trục Ox và M thuộc Ox nên MA + MC ≥ AC.

Dấu “=” xảy ra khi M thuộc AC.

Như vậy M là giao điểm của AC và Ox thì tổng MA + MB đạt giá trị nhỏ nhất bằng AC.

Ta có: $OA=\sqrt{6^2+0^2}=6$, $BC=\sqrt{{\left(6-6\right)}^2+{\left(-3-3\right)}^2}=6$ .  

Gọi D là giao điểm của BC và Ox, khi đó CD = $\frac{1}{2}$ BC = 3 và OA // CD.

Suy ra $\frac{OM}{MD}=\frac{OA}{CD}=\frac{6}{3}=2$. Suy ra OM = 2MD nên OM = $\frac{2}{3}$ OD = $\frac{2}{3}$.6 = 4.

Do đó, M(4; 0).

Vậy M(4; 0) thì tổng MA + MB đạt giá trị nhỏ nhất.

Xem thêm các bài giải Chuyên đề Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Phép dời hình

Bài 2: Phép đồng dạng

Bài 1: Một vài yếu tố của lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton

Bài 2: Một vài ứng dụng của lí thuyết đồ thị

Bài 1: Một số nội dung cơ bản về vẽ kĩ thuật

Bài 2: Đọc và vẽ bản vẽ kĩ thuật đơn giản