Quan sát Hình 42 và chỉ ra hai phép dời hình (phân biệt) biến mỗi tam giác được tô màu thành tam giác
101
23/02/2024
Bài 8 trang 24 Chuyên đề Toán 11: Quan sát Hình 42 và chỉ ra hai phép dời hình (phân biệt) biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
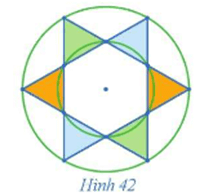
Trả lời
+) Đặt các điểm như hình vẽ.
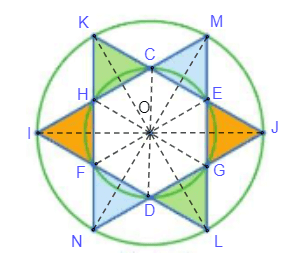
Ta thấy đường tròn nhỏ tâm O có các đường kính CD, EF, GH nên O là trung điểm của CD, EF, GH. Đường tròn lớn tâm O có các đường kính MN, LK, IJ nên O là trung điểm của MN, LK, IJ.
Do đó, ta có phép đối xứng tâm O biến các điểm C, M, E, J, G, L, D tương ứng thành các điểm D, N, F, I, H, K, C.
Từ đó suy ra phép đối xứng tâm O biến các tam giác CME, EJG, GLD, FDN, FHI, KHC tương ứng thành các tam giác DNF, FIH, HKC, ECM, EGJ, LGD hay chính là phép đối xứng tâm O biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
+) Đặt các điểm như hình vẽ:
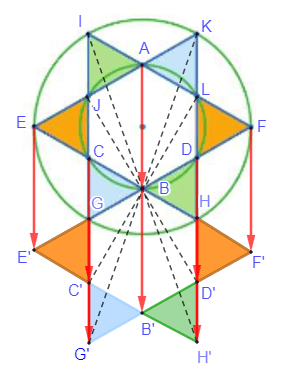
- Phép tịnh tiến theo vectơ →AB biến các tam giác IAJ, EJC, CGB, AKL, LDF, BDH lần lượt thành các tam giác CBG, E'GC', C'G'B', BDH, HD'F', B'D'H'.
- Phép đối xứng tâm B biến các tam giác CBG, E'GC', C'G'B', BDH, HD'F', B'D'H' lần lượt thành các tam giác HBD, FDL, LKA, BGC, CJE, AJI.
Do đó, ta có phép dời hình F có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ →AB và phép đối xứng tâm B ( T→AB trước, ĐB sau) biến các tam giác IAJ, EJC, CGB, AKL, LDF, BDH lần lượt thành các tam giác HBD, FDL, LKA, BGC, CJE, AJI hay chính là phép dời hình F đó biến mỗi tam giác được tô màu thành tam giác cùng màu với nó.
Xem thêm các bài giải Chuyên đề Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Phép dời hình
Bài 2: Phép đồng dạng
Bài 1: Một vài yếu tố của lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton
Bài 2: Một vài ứng dụng của lí thuyết đồ thị
Bài 1: Một số nội dung cơ bản về vẽ kĩ thuật
Bài 2: Đọc và vẽ bản vẽ kĩ thuật đơn giản



