Giải Chuyên đề Toán 11 Bài 2 (Cánh diều): Một vài ứng dụng của lí thuyết đồ thị

Giải Chuyên đề Toán 11 Bài 2: Một vài ứng dụng của lí thuyết đồ thị

I. Vận dụng đồ thị để giải quyết những vấn đề về tìm đường đi ngắn nhất trong những trường hợp đơn giản

Khởi động trang 44 Chuyên đề Toán 11: Như chúng ta đã biết, Lí thuyết đồ thị ra đời trong quá trình khái quát, mô phỏng những vấn đề của khoa học và thực tiễn thành những mô hình toán học. Vì thế, các kết quả của Lí thuyết đồ thị có nhiều ứng dụng trong khoa học và thực tiễn.

Lí thuyết đồ thị có thể giải quyết những vấn đề thực tiễn nào?

Lời giải:

Qua bài học này, ta thấy Lí thuyết đồ thị có thể giải quyết những vấn đề thực tiễn:

- Vấn đề về tìm đường đi ngắn nhất trong những trường hợp đơn giản.

- Vấn đề liên quan đến khoa học tự nhiên và công nghệ.

Hoạt động 1 trang 44 Chuyên đề Toán 11: Giả sử ba địa điểm A, B, C được nối với nhau theo những con đường AB, BC, CA với độ dài lần lượt là 15 km, 20 km, 16 km. Sử dụng đồ thị để mô tả tình huống đó.

Lời giải:

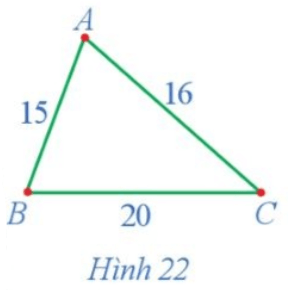
Đồ thị ở Hình 22 mô tả tình huống trong hoạt động này.

Luyện tập 1 trang 44 Chuyên đề Toán 11: Hãy cho ví dụ về đồ thị có trọng số.

Lời giải:

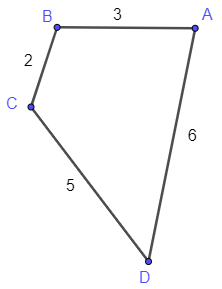
Ví dụ về đồ thị có trọng số: Có 4 trạm xe bus A, B, C, D được nối với nhau theo những con đường AB, BC, CD, DA với độ dài lần lượt là 3 km, 2 km, 5 km, 6 km. Ta có đồ thị mô tả tình huống trên như sau.

Hoạt động 2 trang 44 Chuyên đề Toán 11: Giả sử có sáu địa điểm A, B, C, D, E, F được nối với nhau theo những con đường với độ dài (đơn vị: kilômét) được mô tả bằng đồ thị có trọng số ở Hình 24. Người giao hàng cần đi giao hàng tại sáu địa điểm trên. Người giao hàng xuất phát từ một địa điểm nào đó, đi qua các địa điểm còn lại để giao hàng và trở về địa điểm ban đầu. Hãy tìm một đường đi thỏa mãn điều kiện trên cho người giao hàng sao cho quãng đường mà người giao hàng phải di chuyển là ngắn nhất.

Lời giải:

Để tìm quãng đường đi ngắn nhất trên đồ thị có trọng số, ta áp dụng thuật toán láng giềng gần nhất để tìm tất cả các chu trình xuất phát từ một đỉnh ban đầu, đi qua các đỉnh khác và trở về đỉnh ban đầu sao cho tổng độ dài các cạnh của chu trình đó là ngắn nhất. Sau đó, ta so sánh độ dài của tất cả các chu trình “tốt nhất” vừa tìm được để tìm ra chu trình có tổng độ dài các cạnh là ngắn nhất. Việc giải cụ thể Hoạt động 2 trang 46, ta cùng xem chi tiết ở Luyện tập 2 trang 46.

Luyện tập 2 trang 46 Chuyên đề Toán 11: Sử dụng thuật toán láng giềng gần nhất để giải bài toán trong Hoạt động 2.

Lời giải:

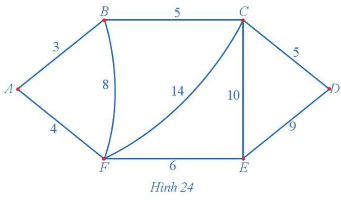
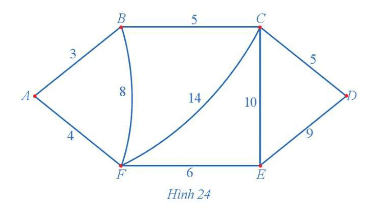
Dễ thấy đồ thị Hình 24 có chu trình Hamilton.

+) Sử dụng thuật toán láng giềng gần nhất đối với đỉnh xuất phát A, ta có:

Từ A, đỉnh gần nhất là B, AB = 3 km;

Từ B, đỉnh chưa đến gần nhất là C, BC = 5 km;

Từ C, đỉnh chưa đến gần nhất là D, CD = 5 km;

Từ D, đỉnh chưa đến gần nhất là E, DE = 9 km;

Từ E, đỉnh chưa đến gần nhất là F, EF = 6 km;

Đến đây không còn đỉnh chưa đến, vì vậy quay về A, FA = 4 km.

Tổng quãng đường theo chu trình ABCDEFA là: 3 + 5 + 5 + 9 + 6 + 4 = 32 (km).

Tương tự bắt đầu với những đỉnh khác, ta có bảng sau:

Vậy người giao hàng chọn 1 đường đi trong 7 đường đi trên thì quãng đường phải di chuyển là ngắn nhất.

II. Vận dụng đồ thị để giải quyết những vấn đề về khoa học tự nhiên và công nghệ

Luyện tập 3 trang 47 Chuyên đề Toán 11: Hexane C₆H₁₄ có năm đồng phân. Vẽ đồ thị tương ứng với năm đồng phân đó.  

Lời giải:

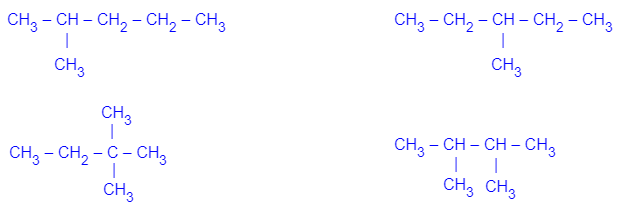
Năm đồng phân của hexane C₆H₁₄ là:

CH₃ – CH₂ – CH₂ – CH₂ – CH₂ – CH₃

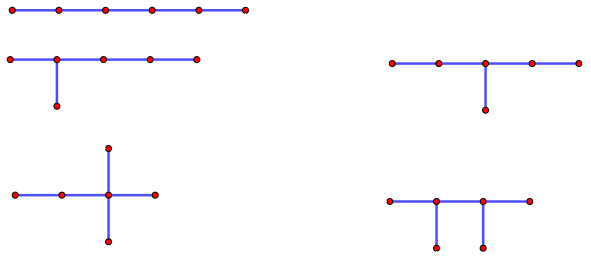
Các đồ thị ở hình dưới đây tương ứng minh họa biểu diễn năm đồng phân của hexane C₆H₁₄. Trong đó các nguyên tử C, CH, CH₂, CH₃ tạo nên các đỉnh của đồ thị, còn các liên kết CH₃ – CH₂, CH₂ – CH₂, CH₂ – CH₃, CH₃ – CH, CH – CH₃, CH – CH₂, CH₂ – C, C – CH₃, CH₂ – CH, CH – CH tạo nên các cạnh của đồ thị.

Bài tập

Bài 1 trang 49 Chuyên đề Toán 11: Hình 31 biểu diễn mạng lưới máy chủ và tốc độ truyền dữ liệu (đơn vị: Megabit/ giây, kí hiệu là Mbps) giữa một số thành phố. Vẽ một đồ thị sử dụng điểm, đường để biểu diễn mạng lưới đó.

Lời giải:

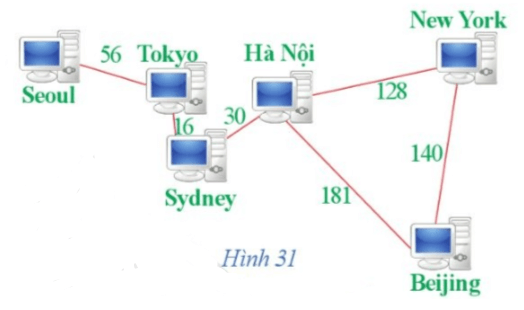
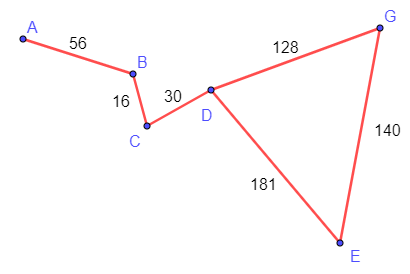
Giả sử các điểm A, B, C, D, E, G lần lượt biểu diễn cho các thành phố Seoul, Tokyo, Sydney, Hà Nội, Beijing, New York.

Ta có đồ thị biểu diễn mạng lưới máy chủ và tốc độ truyền dữ liệu (đơn vị: Megabit/ giây, kí hiệu là Mbps) giữa một số thành phố như sau:

Bài 2 trang 49 Chuyên đề Toán 11: Có bốn địa điểm với độ dài quãng đường giữa các địa điểm (đơn vị: kilômét) mô tả trong Hình 32. Sử dụng thuật toán láng giềng gần nhất, tìm các chu trình xuất phát từ một đỉnh đi qua tất cả các địa điểm, mỗi địa điểm đúng một lần sao cho tổng độ dài các cạnh của chu trình là nhỏ nhất.

Lời giải:

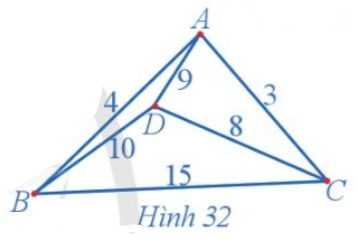
Dễ thấy đồ thị Hình 32 có chu trình Hamilton.

+) Sử dụng thuật toán láng giềng gần nhất đối với đỉnh xuất phát A, ta có:

Từ A, đỉnh gần nhất là C, AC = 3 km;

Từ C, đỉnh chưa đến gần nhất là D, CD = 8 km;

Từ D, đỉnh chưa đến gần nhất là B, DB = 10 km;

Đến đây không còn đỉnh chưa đến, vì vậy quay về A, BA = 4 km.

Tổng quãng đường theo chu trình ACDBA là: 3 + 8 + 10 + 4 = 25 (km).

Tương tự bắt đầu với những đỉnh khác, ta có bảng sau:

Các chu trình trên thỏa mãn điều kiện xuất phát từ một đỉnh đi qua tất cả các địa điểm, mỗi địa điểm đúng một lần và tổng độ dài các cạnh của chu trình là nhỏ nhất.

Bài 3 trang 49 Chuyên đề Toán 11: Giả sử chi phí di chuyển giữa các địa điểm được mô tả ở Hình 33 (đơn vị: nghìn đồng). Ta nên chọn theo chu trình nào đi qua tất cả các địa điểm để tổng chi phí di chuyển là thấp nhất? Chi phí thấp nhất đó bằng bao nhiêu?

Lời giải:

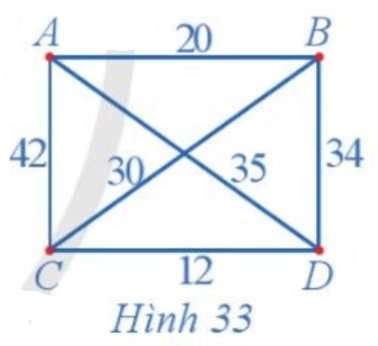
Dễ thấy đồ thị Hình 33 có chu trình Hamilton.

+) Sử dụng thuật toán láng giềng gần nhất đối với đỉnh xuất phát A, ta có:

Từ A, đỉnh gần nhất là B, AB = 20 nghìn đồng;

Từ B, đỉnh chưa đến gần nhất là C, BC = 30 nghìn đồng;

Từ C, đỉnh chưa đến gần nhất là D, CD = 12 nghìn đồng;

Đến đây không còn đỉnh chưa đến, vì vậy quay về A, DA = 35 nghìn đồng.  

Tổng chi phí di chuyển theo chu trình ABCDA là: 20 + 30 + 12 + 35 = 97 (nghìn đồng).

Tương tự bắt đầu với những đỉnh khác, ta có bảng sau:

Vậy có ba chu trình ABCDA, BADCB, DCBAD thỏa mãn đề bài và chi phí thấp nhất là 97 nghìn đồng.

Bài 4 trang 49 Chuyên đề Toán 11: Sử dụng thuật toán láng giềng gần nhất, hãy giải bài toán người giao hàng đối với đồ thị ở Hình 34, số ghi trên mỗi cạnh của đồ thị mô tả độ dài quãng đường giữa các địa điểm (đơn vị: kilômét).

Lời giải:

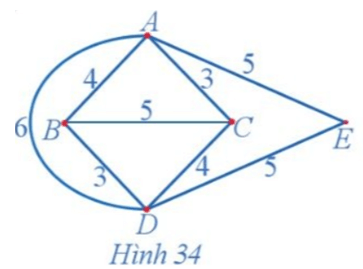
Dễ thấy đồ thị Hình 34 có chu trình Hamilton.

Ta thấy chu trình xuất phát từ đỉnh A là AEDBCA thỏa mãn đề bài với tổng quãng đường nhỏ nhất là AE + ED + DB + BC + CA = 5 + 5 + 3 + 5 + 3 = 21 (km).

Các chu trình xuất phát từ đỉnh B, C, D, E  có 1 đỉnh được đi qua hai lần nên không thỏa mãn quy tắc của thuật toán láng giềng gần nhất nên loại. 

Bài 5 trang 49 Chuyên đề Toán 11: Một nhân viên của bảo tàng nghệ thuật đang có kế hoạch giới thiệu nội dung cuộc triển lãm của bảo tàng đến ba trường học trong khu vực. Người đó muốn đến từng trường và quay trở lại bảo tàng sau khi thăm cả ba trường. Thời gian di chuyển (đơn vị: phút) giữa các trường học và giữa bảo tàng với mỗi trường học được mô tả trong Hình 35.

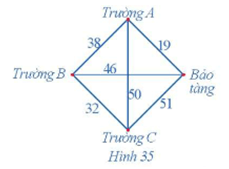
Tìm chu trình xuất phát từ viện bảo tàng sao cho thời gian đi là ít nhất. 

Lời giải:

Từ viện bảo tàng, thời gian di chuyển đến trường A là ngắn nhất: 19 phút.

Từ trường A, thời gian di chuyển đến trường B là ngắn nhất: 38 phút.

Từ trường B, thời gian di chuyển đến trường C là ngắn nhất: 32 phút.

Đến đây, không còn địa điểm nào chưa đi qua nên quay lại viện bảo tàng với thời gian di chuyển: 51 phút.

Do đó, chu trình xuất phát từ viện bảo tàng, qua trường A, trường B, trường C rồi quay lại viện bảo tàng có thời gian đi là ít nhất và thời gian đi là: 19 + 38 + 32 + 51 = 140 (phút).

Xem thêm các bài giải Chuyên đề học tập Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Phép dời hình

Bài 2: Phép đồng dạng

Bài 1: Một vài yếu tố của lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton

Bài 1: Một số nội dung cơ bản về vẽ kĩ thuật

Bài 2: Đọc và vẽ bản vẽ kĩ thuật đơn giản