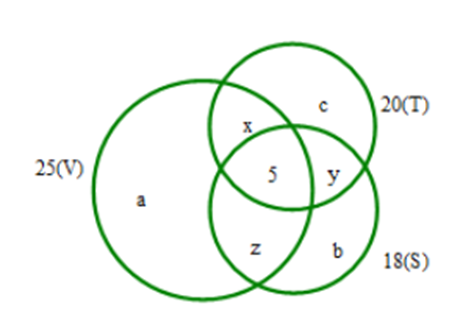
Gọi a, b, c theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán

x là số học sịnh chỉ thích hai môn là văn và toán

y là số học sịnh chỉ thích hai môn là sử và toán

z là số học sịnh chỉ thích hai môn là văn và sử

Ta có số em thích ít nhất một môn là 

45 – 6 = 39

Dựa vào biểu đồ ven ta có hệ phương trình:

\(\left\{ {\begin{array}{*{20}{l}}{a + x + z + 5 = 25{\rm{                     }}\left( 1 \right)}\\{b + y + z + 5 = 18{\rm{                      }}\left( 2 \right)}\\{c + x + y + 5 = 20{\rm{                       }}\left( 3 \right)}\\{x + y + z + a + b + c + 5 = 39{\rm{          }}\left( 4 \right)}\end{array}} \right.\)

Cộng vế với vế (1), (2), (3) ta có

a + b + c + 2 (x + y + z) + 15 = 63 (5)

Từ (4) và (5) ta có

a + b + c + 2(39 – 5 – a – b – c) + 15 = 63

⇔ a + b + c = 20

Suy ra chỉ có 20 em thích chỉ một môn trong ba môn trên

Vậy ta chọn đáp án B.