Trong hệ tọa độ Oxy, cho tam giác ABC có M(2; 3); N(0; -4); P(-1; 6) lần lượt
Trong hệ tọa độ Oxy, cho tam giác ABC có M(2; 3); N(0; –4); P(–1; 6) lần lượt là trung điểm của các cạnh BC; CA; AB. Tìm tọa độ đỉnh A?
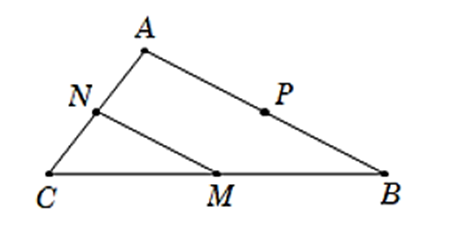
Gọi A(x; y).
Từ giả thiết ta suy ra MN là đường trung bình của tam giác ABC nên:
MN = \(\frac{1}{2}AB = AP = PB\)
Suy ra: \(\overrightarrow {PA} = \overrightarrow {MN} \)(*)
Ta có: \(\overrightarrow {PA} = \left( {x + 1;y - 6} \right);\overrightarrow {MN} = \left( { - 2; - 7} \right)\)
Khi đó (*) ⇔ \(\left\{ \begin{array}{l}x + 1 = - 2\\y - 6 = - 7\end{array} \right.\) ⇔ \(\left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.\)
Suy ra: A(–3;–1).