Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn

Bài 9.12 trang 66 SBT Toán 10 Tập 2: Trên một phố có hai quán ăn A, B. Bốn bạn Sơn, Hải, Văn, Đạo mỗi người chọn ngẫu nhiên một quán ăn.

a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

b) Tính xác suất để:

• Tất cả đều vào một quán;

• Mỗi quán có đúng 2 bạn vào;

• Quán A có 3 bạn vào, quán B có 1 bạn vào;

• Một quán có 3 bạn vào, quán kia có 1 bạn vào.

Trả lời

a) Sơ đồ hình cây mô tả các phần tử của không gian mẫu là:

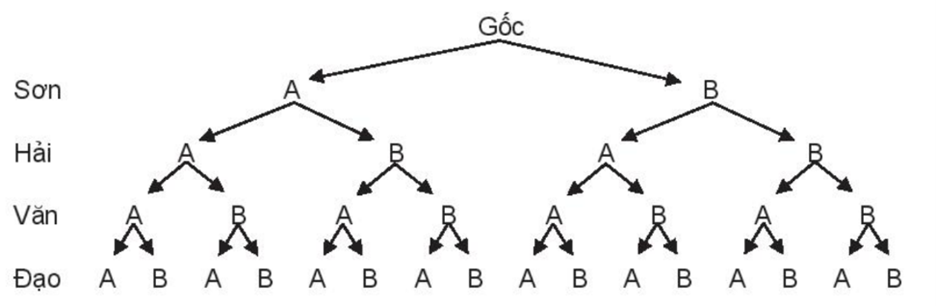
b)

Ta có không gian mẫu:

Ω = {AAAA; AAAB; AABA; AABB; ABAA; ABAB; ABBA; ABBB; BAAA; BAAB; BABA; BABB; BBAA; BBAB; BBBA; BBBB}.

Do đó, n(Ω) = 16.

Gọi biến cố E: “Tất cả đều vào một quán”. Ta có:

E = {AAAA; BBBB}, n(E) = 2, suy ra P(E) = $\frac{n\left(E\right)}{n\left(\Omega \right)}=\frac{2}{16}=\frac{1}{8}$ .

Gọi biến cố F: “Mỗi quán có đúng hai bạn vào”. Ta có:

F = {AABB; ABAB; ABBA; BAAB; BABA; BBAA}, n(F) = 6,

suy ra P(F) = $\frac{n\left(F\right)}{n\left(\Omega \right)}=\frac{6}{16}=\frac{3}{8}$ .

Gọi biến cố G: “Quán A có 3 bạn vào, quán B có 1 bạn vào”. Ta có:

G = {AAAB; AABA; ABAA; BAAA}, n(G) = 4, suy ra P(G) = $\frac{n\left(G\right)}{n\left(\Omega \right)}=\frac{4}{16}=\frac{1}{4}$ .

Gọi biến cố K: “Một quán có 3 bạn vào, quán kia có 1 bạn vào.”. Ta có:

K₁: “Quán A có 3 bạn vào, quán B có 1 bạn vào” nên K₁ = G, n(K₁) = 4.

K₂: “Quán B có 3 bạn vào, quán A có 1 bạn vào”. Ta có:

K₂ = {BBBA; BBAB; BABB; ABBB}, n(K₂) = 4

n(K) = n(K₁) + n(K₂) = 4 + 4 = 8.

Vậy P(K) = $\frac{n\left(K\right)}{n\left(\Omega \right)}=\frac{8}{16}=\frac{1}{2}$ .

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 25: Nhị thức Newton

Ôn tập chương 8

Bài 26: Biến cố và định nghĩa cổ điển của xác suất

Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển

Bài tập cuối chương 9

Bài tập ôn tập cuối năm