Câu hỏi:
18/12/2023 86Bạn Lan để dành được 300 nghìn đồng. Trong một đợt ủng hộ học sinh khó khăn, bạn Lan đã ủng hộ x tờ tiền loại 10 nghìn đồng, y tờ tiền loại 20 nghìn đồng từ tiền để dành của mình. Trong các bất phương trình sau, bất phương trình nào diễn tả giới hạn về tổng số tiền mà bạn Lan đã ủng hộ.
A. x + y < 300 ;
B. 10x + y < 300 ;
C. 10x + 20y > 300;
D. 10x + 20y ≤ 300.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Số tiền mệnh giá 10 nghìn đồng là: 10x (nghìn đồng)
Số tiền mệnh giá 20 nghìn đồng là: 20y (nghìn đồng)
Tổng số tiền bạn Lan đã ủng hộ là: 10x + 20y (nghìn đồng).
Vì tổng số tiền Lan ủng hộ không vượt quá số tiền Lan để dành được là 300 nghìn đồng nên ta có bất phương trình: 10x + 20y ≤ 300.
Vậy ta chọn đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hệ bất phương trình \(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
Cho hệ bất phương trình \(\left\{ \begin{array}{l} - x + 2y \ge 2\\2x + y \le - 1\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
Câu 2:
Một công ty dự định sản xuất hai loại sản phẩm I và II. Các sản phẩm này được chế tạo từ hai loại nguyên liệu A, B. Số kilôgam dự trữ từng loại nguyên liệu và số kilôgam từng loại cần dùng để sản xuất 1 kg sản phẩm được cho trong bảng sau :
Loại nguyên liệu
Số kilôgam nguyên liệu dự trữ
Số kilôgam nguyên liệu cần dùng sản xuất 1 kg sản phẩm
I
II
A
8
2
1
B
12
2
2
Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất ? Biết rằng, mỗi kilogam sản phẩm loại I lãi 10 triệu đồng, mỗi sản phẩm loại II lãi 20 triệu đồng.
Một công ty dự định sản xuất hai loại sản phẩm I và II. Các sản phẩm này được chế tạo từ hai loại nguyên liệu A, B. Số kilôgam dự trữ từng loại nguyên liệu và số kilôgam từng loại cần dùng để sản xuất 1 kg sản phẩm được cho trong bảng sau :
|
Loại nguyên liệu |
Số kilôgam nguyên liệu dự trữ |
Số kilôgam nguyên liệu cần dùng sản xuất 1 kg sản phẩm |
|
|
I |
II |
||
|
A |
8 |
2 |
1 |
|
B |
12 |
2 |
2 |
Công ty đó nên sản xuất bao nhiêu sản phẩm mỗi loại để tiền lãi thu về lớn nhất ? Biết rằng, mỗi kilogam sản phẩm loại I lãi 10 triệu đồng, mỗi sản phẩm loại II lãi 20 triệu đồng.
Câu 3:
Một người nông dân dự định quy hoạch x sào đất trồng rau cải và y sào đất trồng cà chua. Biết rằng người nông dân chỉ có tối đa 900 nghìn đồng để mua hạt giống và giá tiền hạt giống cho mỗi sào đất trồng rau cải là 100 nghìn đồng, mỗi sào đất trồng cà chua là 50 nghìn đồng. Trong các hệ bất phương trình sau, hệ nào mô tả các ràng buộc đối với x, y ?
Câu 5:
Miền nghiệm của bất phương trình: –3x + y > 0 chứa điểm nào trong các điểm sau:
Miền nghiệm của bất phương trình: –3x + y > 0 chứa điểm nào trong các điểm sau:
Câu 6:
Điểm A(1; –3) là điểm thuộc miền nghiệm của bất phương trình nào?
Câu 7:
Cho bất phương trình x + y ≤ 2 (1). Chọn khẳng định đúng trong các khẳng định sau:
D. Bất phương trình (1) vô nghiệm.
Câu 8:
Bất phương trình nào tương đương với bất phương trình 3x – y > 7(x – 4y) + 1?
Câu 10:
Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn ?
Câu 11:
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Câu 12:
Giá trị nhỏ nhất Fmin của biểu thức F= –x + y trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{c}}{ - 2x + y \ge 2}\\{y - x \le 4}\\{x + 2y \ge 5}\end{array}} \right.\) là:
Câu 13:
Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình:
4(2 – y) > 2x + y – 2.
Câu 14:
Miền không gạch trong hình vẽ sau (bao gồm cả bờ), biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
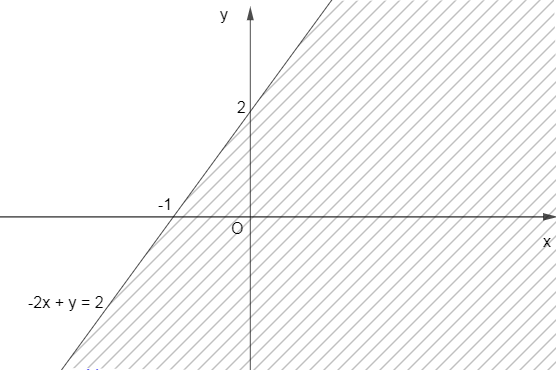
Câu 15:
Cho hệ \[\left\{ \begin{array}{l}x + y \le 1\\4x\,\, - \,y\, \le 2\\x \ge 0\end{array} \right.\]. Giá trị lớn nhất của biểu thức P = x – y trên miền nghiệm của hệ đã cho là:
Cho hệ \[\left\{ \begin{array}{l}x + y \le 1\\4x\,\, - \,y\, \le 2\\x \ge 0\end{array} \right.\]. Giá trị lớn nhất của biểu thức P = x – y trên miền nghiệm của hệ đã cho là:


