Câu hỏi:
21/12/2023 94Cho các số 0; 1; 2; 3; 4. Lập được bao nhiêu số có bốn chữ số khác nhau từ các số đã cho.
A. 32;
B. 120;
C. 60;
D. 96.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Có 4 cách chọn chữ số hàng nghìn (do số 0 không thể đứng ở chữ số hàng nghìn)
Có 4 cách chọn chữ số hàng trăm (do phải khác với chữ số hàng nghìn)
Có 3 cách chọn chữ số hàng chục (do phải khác với chữ số hàng nghìn, hàng trăm)
Có 2 cách chọn chữ số hàng đơn vị (do phải khác với chữ số hàng nghìn, chữ số hàng trăm, chữ số hàng chục)
Số các số có bốn chữ số khác nhau được lập từ các số đã cho là:
4 . 4 . 3 . 2 = 96 (số).
Hướng dẫn giải
Đáp án đúng là: D
Có 4 cách chọn chữ số hàng nghìn (do số 0 không thể đứng ở chữ số hàng nghìn)
Có 4 cách chọn chữ số hàng trăm (do phải khác với chữ số hàng nghìn)
Có 3 cách chọn chữ số hàng chục (do phải khác với chữ số hàng nghìn, hàng trăm)
Có 2 cách chọn chữ số hàng đơn vị (do phải khác với chữ số hàng nghìn, chữ số hàng trăm, chữ số hàng chục)
Số các số có bốn chữ số khác nhau được lập từ các số đã cho là:
4 . 4 . 3 . 2 = 96 (số).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tập hợp A = {0; 1; 2; 3; 4; 5}. Có thể lập bao nhiêu số tự nhiên có 3 chữ số khác nhau và chia hết cho 5?
Câu 2:
Cho tập hợp các số {0; 1; 2; 3; 4; 5; 6}. Có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số sao cho các chữ số đôi một khác nhau.
Câu 3:
Các thành phố A; B; C; D được nối với nhau bởi các con đường như hình vẽ sau:
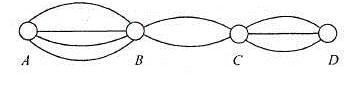
Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
Câu 5:
Để đi từ thành phố A đến thành phố B có 3 con đường, để đi từ thành phố B đến thành phố C có 5 con đường. Đi từ thành phố C đến thành phố D có 2 con đường. Hỏi có bao nhiêu cách đi từ thành phố A đến D sao cho chỉ đi qua thành phố B và thành phố C một lần.
Câu 6:
Cho tập A = {0; 1; 3; 5; 7}. Có thể lập được bao nhiêu số tự nhiên có 4 chữ số sao cho các chữ số đó đôi một khác nhau và là số chẵn.
Câu 7:
Có 10 lớp khối 10, mỗi lớp cử 1 bạn nam và 1 bạn nữ đi tham gia đại hội Đoàn trường. Trong kỳ đại hội, cán bộ đoàn chọn một bạn nam và một bạn nữ lên phát biểu. Hỏi có tổng số bao nhiêu cách chọn?


