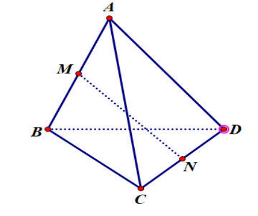
Ta có: \(\overrightarrow {MN}  = \frac{1}{2}\left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right) \Rightarrow {\left| {\overrightarrow {MN} } \right|^2} = \frac{1}{4}\left( {{{\overrightarrow {AC} }^2} + 2\overrightarrow {AC} .\overrightarrow {BD}  + {{\overrightarrow {BD} }^2}} \right)\)

                                                           $= \frac{1}{4}\left( {2{a^2} + 2\overrightarrow {AC} .\overrightarrow {BD} } \right).$

Mà: $\overrightarrow {AC} .\overrightarrow {BD}  = \overrightarrow {AC} .\left( {\overrightarrow {AD}  - \overrightarrow {AB} } \right) = \overrightarrow {AC} .\overrightarrow {AD}  - \overrightarrow {AC} .\overrightarrow {AB}$

$= \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AD} } \right|.\cos 60^\circ  - \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AB} } \right|.\cos 60^\circ  = 0.$

Suy ra ${\left| {\overrightarrow {MN} } \right|^2} = \frac{1}{4}.2{a^2} = \frac{{{a^2}}}{2}$$\Rightarrow \left| {\overrightarrow {MN} } \right| = \frac{{a\sqrt 2 }}{2}.$

Ta có: \(\overrightarrow {AC} .\overrightarrow {MN}  = \frac{1}{2}\overrightarrow {AC} .\left( {\overrightarrow {AC}  + \overrightarrow {BD} } \right) = \frac{1}{2}\left( {{{\overrightarrow {AC} }^2} + \overrightarrow {AC} .\overrightarrow {BD} } \right) = \frac{{{a^2}}}{2}.\)

Khi đó, \(\cos \left( {\overrightarrow {AC} ,\overrightarrow {MN} } \right) = \frac{{\overrightarrow {AC} .\overrightarrow {MN} }}{{\left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {MN} } \right|}} = \frac{{\frac{{{a^2}}}{2}}}{{a.\frac{{a\sqrt 2 }}{2}}} = \frac{{\sqrt 2 }}{2}.\)

Vậy $\cos \left( {\overrightarrow {AC} ,\overrightarrow {MN} } \right) = \frac{{\sqrt 2 }}{2}.$