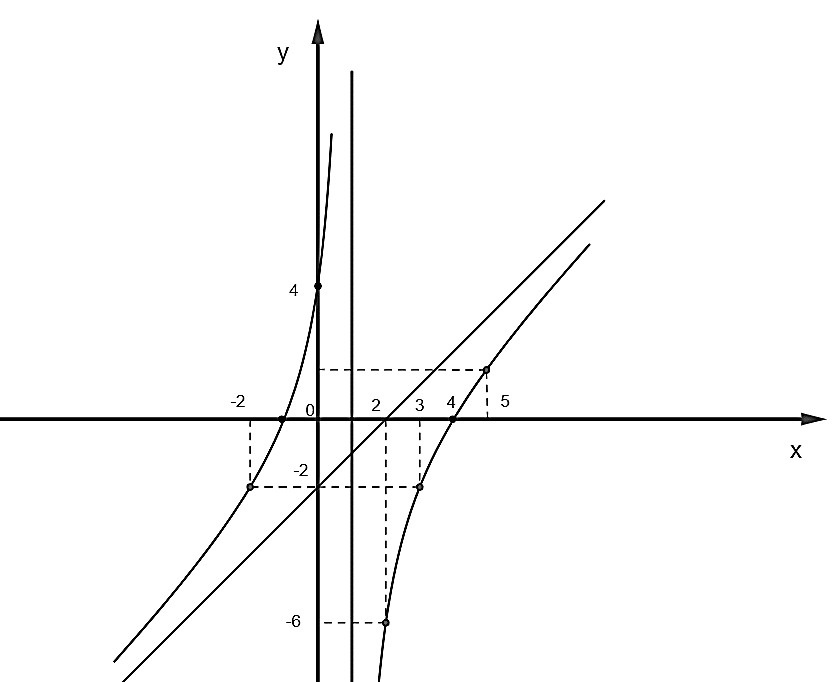
Cho hàm số (X) y = (x^2 - 3x + m) / (x - 1)
Cho hàm số (C): y=x2−3x+mx−1.
Khảo sát và vẽ đồ thị hàm số (C) với m=−4.
Cho hàm số (C): y=x2−3x+mx−1.
Khảo sát và vẽ đồ thị hàm số (C) với m=−4.
Với m=−4, ta có: (C):y=x2−3x−4x−1.
1. Tập xác định: D=R∖{1}.
2. Sự biến thiên
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
lim
\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} - 3x - 4}}{{x - 1}} = - \infty .
Do đó, đồ thị hàm số không có tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 3x - 4}}{{x - 1}} = - \infty ,\)\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{{x^2} - 3x - 4}}{{x - 1}} = + \infty , do đó đồ thị hàm số nhận đường thẳng x = 1 làm tiệm cận đứng.
\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 3x - 4}}{{x\left( {x - 1} \right)}} = 1, \mathop {\lim }\limits_{x \to + \infty } \left[ {\frac{{{x^2} - 3x - 4}}{{x - 1}} - x} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 2x - 4}}{{x - 1}} = - 2.
Do đó, đồ thị hàm số nhận đường thẳng y = x - 2 làm tiệm cận xiên.
Ta có: y' = \frac{{{x^2} - 2x + 7}}{{{{\left( {x - 1} \right)}^2}}} > 0,\forall x \in D.
Từ đây ta có bảng biến thiên:
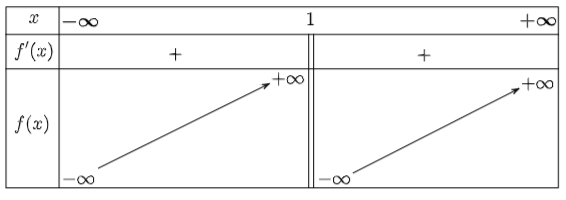
Hàm số đồng biến trên các khoảng \left( { - \infty ;1} \right) và \left( {1; + \infty } \right).
Hàm số không có cực trị.
3. Đồ thị
Giao điểm của đồ thị với trục tung: \left( {0;4} \right).
Giao điểm của đồ thị với trục hoành: \left( {4;0} \right),\left( { - 1;0} \right).
Đồ thị đi qua các điểm \left( { - 2; - 2} \right);\left( {2; - 6} \right);\left( {3; - 2} \right);\left( {5;\frac{3}{2}} \right).
Đồ thị nhận đường thẳng x = 1 làm tiệm cận đứng và đường thẳng y = x - 2 làm tiệm cận xiên.
Ta có đồ thị hàm số: