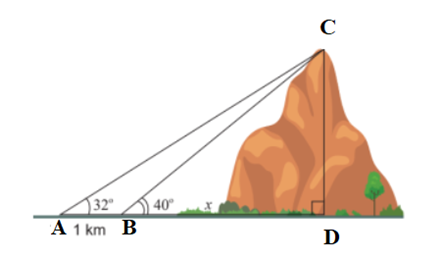
Tính chiều cao của một ngọn núi DC cho biết tại hai điểm A, B cách nhau 1km trên mặt đất ta nhìn thấy đỉnh núi với góc nâng lần lượt là 40° và 32° (làm tròn đến hai chữ số thập phân).

Đặt BD = x km, khi đó ta có AD = BD + BA = x + 1.

Trong tam giác ACD vuông tại D ta có: tan\(\widehat {CAD} = \tan 32^\circ = \frac{{CD}}{{AD}} = \frac{{CD}}{{x + 1}}\)

⇒ CD = tan32°.(x + 1) (1)

Trong tam giác CBD vuông tại D ta có:

tan\(\widehat {CBD} = \tan 40^\circ = \frac{{CD}}{{BD}} = \frac{{CD}}{x}\)

⇒ CD = tan40°.x (2)

Từ (1) và (2) suy ra: 

tan32°.(x + 1) = tan40°.x

⇒ x = \(\frac{{\tan 32^\circ }}{{\tan 40^\circ - \tan 32^\circ }} \approx 2,92\)(km)

Suy ra CD = x.tan40° ≈ 2,92.tan40° ≈ 2,45 km.

Vậy chiều cao CD của một ngọn núi khoảng 2,45 km.