Tính bán kính đường tròn ngoại tiếp tam giác đều cạnh a
Tính bán kính đường tròn ngoại tiếp tam giác đều cạnh a.
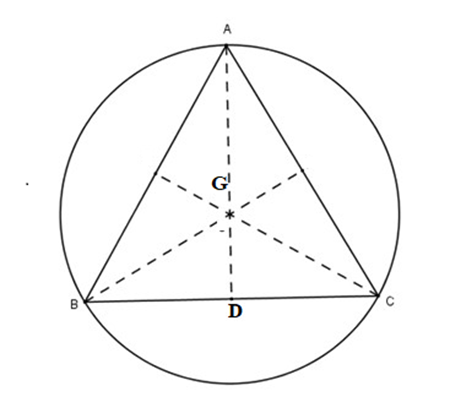
Tam giác đều có trọng tâm, trực tâm, tâm đường tròn ngoại tiếp trùng nhau
Gọi G là trọng tâm của tam giác đều ABC thì G cũng là tâm đường tròn ngoại tiếp tam giác ABC
Ta có: R = GA = GB = GC
Kẻ trung tuyến AD của tam giác suy ra A,G,D thẳng hàng và \(AG = \frac{2}{3}AD\)
AD cũng là đường cao trong tam giác đều, do đó:
AD2 + DB2 = AB2
⇔ AD2 + \({\left( {\frac{a}{2}} \right)^2} = {a^2}\)
⇔ AD = \(\frac{{a\sqrt 3 }}{2}\)
R = \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)