Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình \(\log _2^2x + 4{\log _2}x - m = 0\) có nghiệm thuộc khoảng (0; 1).

A. (–4; +∞)

B. [–4; +∞)

C. [–4; 0)

D. [–2; 0].

Đáp án đúng là: B

Đặt t = log₂x

Suy ra t ∈ (–∞; 0)

Khi đó ta có phương trình ẩn t

t² + 4t – m = 0

⇔ t² + 4t = m

Xét f(t) = t² + 4t

f’(t) = 2t + 4

f’(t) = 0 ⇔ 2t + 4 = 0 ⇔ t = –2

Ta có bảng biến thiên:

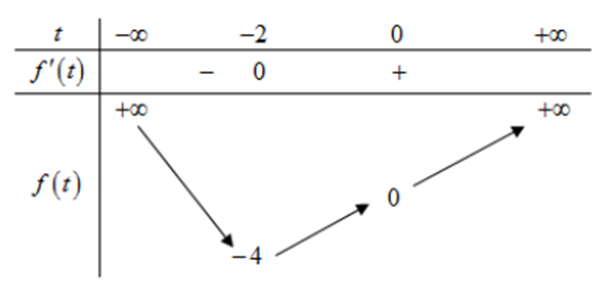
Với t ∈ (–∞; 0) suy ra m ∈ [–4; +∞) thì phương trình \(\log _2^2x + 4{\log _2}x - m = 0\) có nghiệm thuộc khoảng (0; 1)

Vậy ta chọn đáp án B.