Tìm m để phương trình log^2 x + log x − m = 0 có 2 nghiệm phân biệt thuộc khoảng (0; 1).
Tìm m để phương trình log2 x + log x − m = 0 có 2 nghiệm phân biệt thuộc khoảng (0; 1).
Lời giải
Đặt t = log x. Với x Î (0; 1) Þ t Î (−∞; 0).
Phương trình đã cho trở thành:
t2 + t − m = 0
Û t2 + t = m
Xét bảng biến thiên:
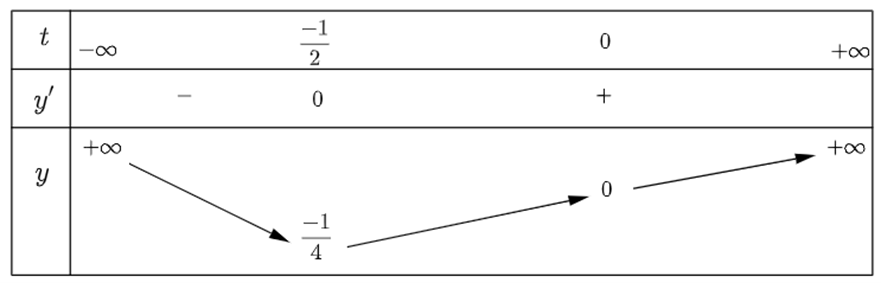
Để phương trình có hai nghiệm x phân biệt thuộc khoảng (0; 1) thì có hai nghiệm t phân biệt thuộc khoảng t Î (−∞; 0)
\( \Rightarrow \frac{{ - 1}}{4} < m < 0\)
Vậy \(m \in \left( { - \frac{1}{4};\;0} \right)\) là giá trị của m thỏa mãn.