Tìm GTNN của biểu thức A = \(\frac{{6x + 1}}{{12{x^2} + 1}}\).

Đặt f(x) = \(\frac{{6x + 1}}{{12{x^2} + 1}}\)

⇔ \[f'\left( x \right) = \frac{{6\left( {12{x^2} + 1} \right) - \left( {6x + 1} \right).24x}}{{{{\left( {12{x^2} + 1} \right)}^2}}} = \frac{{ - 72{x^2} - 24x + 6}}{{{{\left( {12{x^2} + 1} \right)}^2}}}\]

Xét f'(x) = 0 suy ra: –72x² – 24x + 6 = 0

⇔ –24x² – 4x + 1 = 0

⇔ \(\left[ \begin{array}{l}x = \frac{1}{6}\\x = \frac{{ - 1}}{2}\end{array} \right.\)

 Ta có bảng biến thiên:

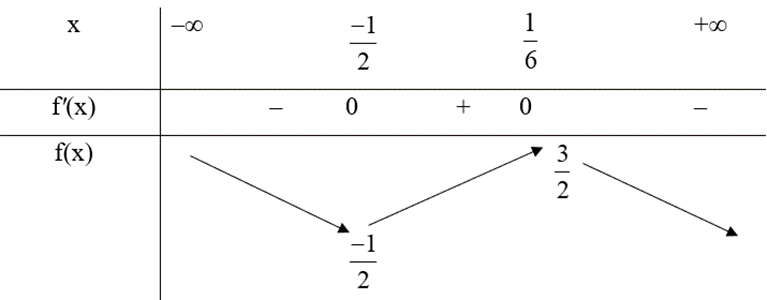
Vậy GTNN của A là \(\frac{{ - 1}}{2}\) khi x = \(\frac{{ - 1}}{2}\).