Tìm các giá trị nguyên của m để phương trình \({\cos ^2}x + \sqrt {\cos x + m} = m\) có nghiệm.

Ta có: \({\cos ^2}x + \sqrt {\cos x + m} = m\) ⇒ m ≥ 0.

Đặt \(\sqrt {\cos x + m} = t,t \ge 0.\)

Phương trình trở thành: \(\left\{ {\begin{array}{*{20}{c}}{{{\cos }^2}x + t = m}\\{{t^2} - \cos x = m}\end{array}} \right.\)

⇒ (cos²x – t²) + (t + cos x) = 0

⇔ (cos x + t)(cos x – t + 1) = 0

⇔ \(\left[ {\begin{array}{*{20}{c}}{\cos x = - t}\\{\cos x - t + 1 = 0}\end{array}} \right.\)

TH1: cos x = -t

⇒ \(\sqrt {\cos x + m} = - \cos x\) ⇔ \(\left\{ {\begin{array}{*{20}{c}}{\cos x \le 0}\\{{{\cos }^2}x - \cos x = m}\end{array}} \right.\)

Đặt u = cos x (-1 ≤ u ≤ 0)

Xét hàm số f(u) = u² – u trên đoạn [-1; 0], có hoành độ đỉnh \(x = \frac{1}{2} \notin \left[ { - 1;0} \right]\) và bảng biến thiên:

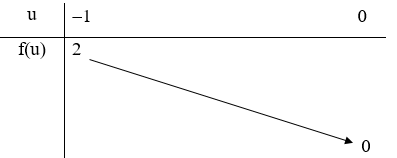
Để phương trình có nghiệm thì m ∈ [0; 2]. Vì m ∈ ℤ nên m ∈ {0; 1; 2}.

TH2: cos x – t + 1 = 0

⇔ \(\sqrt {\cos x + m} = 1 + \cos x\)

⇔ cos²x + cos x + 1 = m

Đặt v = cos x, -1 ≤ v ≤ 1. Ta có m = v² + v + 1 = g(v)

Hàm số bậc hai g(v) có hoành độ đỉnh \(v = \frac{1}{2} \in \left[ { - 1;1} \right]\) và có bảng biến thiên:

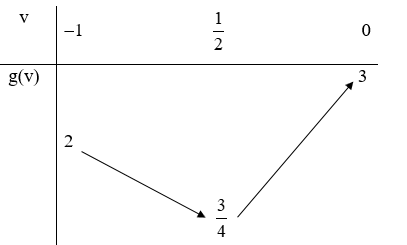
Để phương trình có nghiệm thì \(m \in \left[ {\frac{3}{4};3} \right].\) Vì m ∈ ℤ nên m ∈ {1; 2; 3}.

Vậy có tất cả 4 số nguyên m thỏa mãn bài toán.