Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Tia phân giác của \[\widehat {ABC}\] cắt AC tại D.

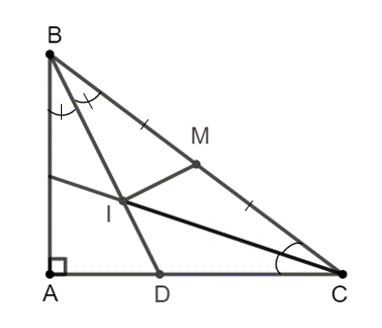
Xét ∆ABD vuông tại A, áp dụng định lý Pythagore, ta có:

BD² = AB² + AD² = 6² + 3² = 45 , suy ra \[BD = 3\sqrt 5 \] (cm).

Ta có CI là đường phân giác của \[\widehat {DCB}\] trong ∆CBD nên

\[\frac{{ID}}{{IB}} = \frac{{CD}}{{CB}} = \frac{5}{{10}} = \frac{1}{2}\] hay \[\frac{{ID}}{1} = \frac{{IB}}{2}\].

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\[\frac{{ID}}{1} = \frac{{IB}}{2} = \frac{{ID + IB}}{{1 + 2}} = \frac{{BD}}{3} = \frac{{3\sqrt 5 }}{3} = \sqrt 5 \].

Suy ra ID = \[\sqrt 5 \](cm) và IB = 2\[\sqrt 5 \](cm).

Ta có: MB = MC = \[\frac{1}{2}\]BC = 5 (cm)

Xét ∆IDC và ∆IMC có

IC chung

\[\widehat {DCI} = \widehat {MCI}\]

DC = MC

Do đó ∆IDC = ∆IMC (c.g.c).

Suy ra ID = IM = \[\sqrt 5 \](cm)

Ta có IM² + IB² = \[{\left( {\sqrt 5 } \right)^2} + {\left( {2\sqrt 5 } \right)^2}\]= 25 và MB² = 5² = 25.

Do đó IM² + IB² = MB².

Áp dụng định lý Pythagore đảo trong ∆IBM, suy ra ∆IBM vuông tại I.

Suy ra \[\widehat {BIM}\]= 90°.