Cho hình thang ABCD (AB // CD) và DE = EC (Hình 8). Gọi O là giao điểm của AC và BD, K là giao điểm của EO và AB. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?

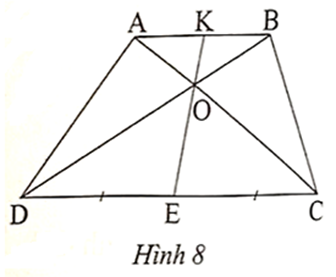
(I) \[\frac{{AK}}{{EC}} = \frac{{KB}}{{DE}}\];

(II) AK = KB ;

(III) \[\frac{{AO}}{{AC}} = \frac{{AB}}{{DC}}\];

(IV) \[\frac{{AK}}{{EC}} = \frac{{OB}}{{OD}}\].

A. 1;

B. 2;

C. 3;

D. 4.

Đáp án đúng là: C

Theo hệ quả của định lí Thalès:

• Xét ∆OEC có AK // EC nên \[\frac{{AK}}{{EC}} = \frac{{BK}}{{DE}}\].

• Xét ∆OED có BK // DE nên \[\frac{{BK}}{{DE}} = \frac{{OK}}{{KE}}\].

Suy ra \[\frac{{AK}}{{EC}} = \frac{{BK}}{{DE}}\].

Mà EC = DE , suy ra AK = BK.

Xét ∆OCD có AB // CD, theo hệ quả của định lí Thalès, ta có:

\[\frac{{AO}}{{AC}} = \frac{{AB}}{{DC}} = \frac{{OB}}{{OD}}\].

Vậy có 3 khẳng định đúng là các khẳng định (I), (II), (III).