Cho tam giác ABC có I ∈ AB và K ∈ AC. Kẻ IM // BK (M ∈ AC), KN // CI (N thuộc
Cho tam giác ABC có I ∈ AB và K ∈ AC. Kẻ IM // BK (M ∈ AC), KN // CI (N ∈ AB). Chứng minh MN // BC.
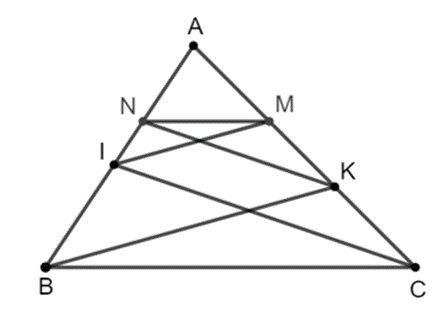
• Xét ∆ABK có IM // BK, theo định lí Thalès, ta có \[\frac{{AI}}{{AB}} = \frac{{AM}}{{AK}}\].
• Xét ∆AIC có KN // CI, theo định lí Thalès, ta có \[\frac{{AN}}{{AI}} = \frac{{AK}}{{AC}}\].
Do đó \[\frac{{AI}}{{AB}} \cdot \frac{{AN}}{{AI}} = \frac{{AM}}{{AK}} \cdot \frac{{AK}}{{AC}}\], suy ra \[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\].
Xét ∆ABC có \[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\], theo định lí Thalès đảo ta có MN // BC.