A. S_MNPQ = \[\frac{1}{4}\]S_ABCD ;

B. S_MNPQ = \[\frac{1}{3}\]S_ABCD ;

C. S_MNPQ = S_ABCD ;

D. S_MNPQ = \[\frac{1}{2}\]S_ABCD .

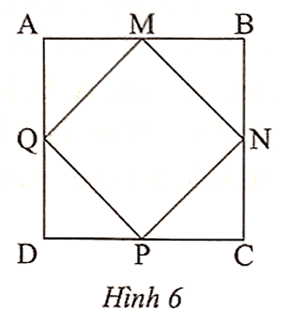
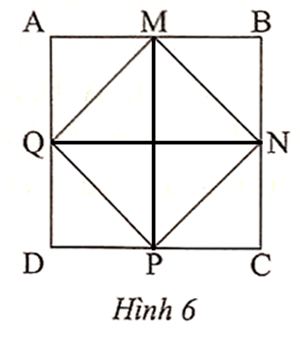
Vì ABCD là hình vuông và M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên

AM = MB = BN = NC = CP = PD = DQ = QA.

Suy ra AM² + QA² = MB² + BN² = NC² + CP² = PD² + DQ²,

Khi đó MQ² = MN² = NP² = PQ² hay MQ = MN = NP = PQ,

Do đó tứ giác MNPQ là hình thoi       (1)

• Vì AM = AQ nên ∆AMQ vuông cân tại A, suy ra \[\widehat {AMQ}\] = 45°.

• Vì BM = BN nên ∆BMN vuông cân tại B, suy ra \[\widehat {BMN}\] = 45°.

Mà \[\widehat {AMQ}\]+ \[\widehat {QMN}\] + \[\widehat {BMN}\] = 180°, suy ra \[\widehat {QMN}\] = 90°       (2)

Từ (1) và (2) suy ra MNPQ là hình vuông.

 S_ABCD = AB² ; S_MNPQ = MQ²

MQ² = AM² + QA² = \[{\left( {\frac{1}{2}AB} \right)^2}\]+ \[{\left( {\frac{1}{2}AD} \right)^2}\]

= \[\frac{1}{4}\]AB² + \[\frac{1}{4}\]AD² = \[\frac{1}{4}\]AB² + \[\frac{1}{4}\]AB² = \[\frac{1}{2}\]AB².

Do đó S_MNPQ = \[\frac{1}{2}\]S_ABCD.