Tập hợp tất cả các giá trị của tham số m để phương trình 4 ( sin ^4 x+ cos ^ 4 x ) + sin ^2 2x + 4m = 4 cos 2x
22
17/11/2024
Tập hợp tất cả các giá trị của tham số m để phương trình 4(sin4x+cos4x)+sin22x+4m=4cos2x có nghiệm là đoạn [a; b]. Tính 2b- a
A. 2.
B. 3.
C. 1.
D. 4.
Trả lời
Ta có: 4(sin4x+cos4x)+sin22x+4m=4cos2x
⇔4[(sin2x+cos2x)2−2sin2xcos2x]+sin22x−4cos2x+4m=0
⇔4−sin22x−4cos2x+4m=0⇔cos22x−4cos2x=−4m−3
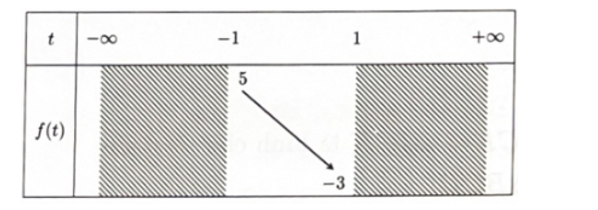
Đặt t=cos2x(t∈[−1;1]). Ta có phương trình t2−4t=−4m−3 (*) với t∈[−1;1].
Phương trình đã cho có nghiệm x khi và chỉ khi phương trình (*) có nghiệm t∈[−1;1]..
Lập bảng biến thiên của hàm f(t)=t2−4t trên [−1;1].
Từ bảng biến thiên ta thấy phương trình có nghiệm t∈[−1;1] khi và chỉ khi
−3≤−4m−3≤5⇔−2≤m≤0. Vậy a=−2;b=0 suy ra 2b - a = 0
Chọn A