Câu hỏi:
01/02/2024 42Tam giác ABC có trung tuyến CI bằng nửa cạnh AB. Số đo góc ACB là:
A. 90°;
B. 60°;
C. 45°;
D. 30°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
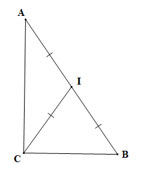
Ta có CI = \(\frac{1}{2}\)AB (giả thiết), IA = IB (vì I là trung điểm của AB).
Nên AI = BI = CI
Xét DIBC có IB = IC nên tam giác IBC cân tại I.
Suy ra \(\widehat {ICB} = \widehat {IBC}\)
Xét DIAC có IA = IC nên tam giác IAC cân tại I
Suy ra \(\widehat {ICA} = \widehat {IAC}\)
Xét DABC có \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \) (tổng ba góc trong một tam giác)
Hay \(\widehat {IBC} + \widehat {IAC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \)
Mà \(\widehat {ICB} = \widehat {IBC}\),\(\widehat {ICA} = \widehat {IAC}\) (chứng minh trên)
Suy ra \(2(\widehat {ICB} + \widehat {ACI}) = 180^\circ \)
Do đó \(\widehat {ACB} = 180^\circ :2 = 90^\circ \)
Vậy ta chọn phương án A.
Hướng dẫn giải
Đáp án đúng là: A

Ta có CI = \(\frac{1}{2}\)AB (giả thiết), IA = IB (vì I là trung điểm của AB).
Nên AI = BI = CI
Xét DIBC có IB = IC nên tam giác IBC cân tại I.
Suy ra \(\widehat {ICB} = \widehat {IBC}\)
Xét DIAC có IA = IC nên tam giác IAC cân tại I
Suy ra \(\widehat {ICA} = \widehat {IAC}\)
Xét DABC có \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \) (tổng ba góc trong một tam giác)
Hay \(\widehat {IBC} + \widehat {IAC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \)
Mà \(\widehat {ICB} = \widehat {IBC}\),\(\widehat {ICA} = \widehat {IAC}\) (chứng minh trên)
Suy ra \(2(\widehat {ICB} + \widehat {ACI}) = 180^\circ \)
Do đó \(\widehat {ACB} = 180^\circ :2 = 90^\circ \)
Vậy ta chọn phương án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC cân tại A có trung tuyến BD và CE cắt nhau tại G. Khẳng định nào sau đây là sai?
Câu 2:
Cho ∆ABC có AD, BE, CF là ba đường trung tuyến và trọng tâm G.
Cho các phát biểu sau:
(I) \[AD + BE + CF > \frac{3}{4}\left( {AB + BC + AC} \right)\];
(II) AD + BE + CF < AB + BC + AC.
Chọn khẳng định đúng:


