Trắc nghiệm Toán 7 CTST Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án (Phần 2)
Trắc nghiệm Toán 7 CTST Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án (Phần 2) (Vận dụng)
-
203 lượt thi
-
3 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Tam giác ABC có trung tuyến CI bằng nửa cạnh AB. Số đo góc ACB là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
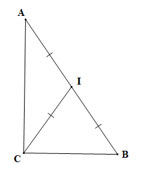
Ta có CI = \(\frac{1}{2}\)AB (giả thiết), IA = IB (vì I là trung điểm của AB).
Nên AI = BI = CI
Xét DIBC có IB = IC nên tam giác IBC cân tại I.
Suy ra \(\widehat {ICB} = \widehat {IBC}\)
Xét DIAC có IA = IC nên tam giác IAC cân tại I
Suy ra \(\widehat {ICA} = \widehat {IAC}\)
Xét DABC có \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \) (tổng ba góc trong một tam giác)
Hay \(\widehat {IBC} + \widehat {IAC} + \widehat {ICB} + \widehat {ICA} = 180^\circ \)
Mà \(\widehat {ICB} = \widehat {IBC}\),\(\widehat {ICA} = \widehat {IAC}\) (chứng minh trên)
Suy ra \(2(\widehat {ICB} + \widehat {ACI}) = 180^\circ \)
Do đó \(\widehat {ACB} = 180^\circ :2 = 90^\circ \)
Vậy ta chọn phương án A.
Câu 2:
Cho tam giác ABC cân tại A có trung tuyến BD và CE cắt nhau tại G. Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
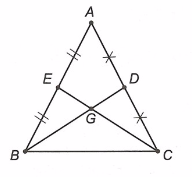
• Vì D là trung điểm của AC nên AD = DC = \(\frac{1}{2}\)AC.
Vì E là trung điểm của AB nên AE = EB = \(\frac{1}{2}\)AB.
Mà AB = AC (do DABC cân tại A)
Suy ra AE = AD = BE = CD. Do đó phương án C là đúng.
• Xét DEBC và DDCB có:
BE = CD (chứng minh trên),
\(\widehat {DCB} = \widehat {EBC}\)(do DABC cân tại A),
BC là cạnh chung
Do đó DEBC = DDCB (c.g.c)
Suy ra EC = BD (hai cạnh tương ứng)
Xét DABC có trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm tam giác ABC.
Suy ra EG = \(\frac{1}{3}\)CE và GD = \(\frac{1}{3}\)BD
Mà BD = EC (chứng minh trên) nên EG = \(\frac{1}{3}\)BD hay BD = 3EG
Do đó phương án D là đúng.
• Ta có EG = \(\frac{1}{3}\)CE và GD = \(\frac{1}{3}\)BD
Mà BD = EC nên EG = GD.
Suy ra G nằm trên đường trung trực của ED.
Lại có AE = AD nên A cũng nằm trên đường trung trực của ED.
Do đó AG là đường trung trực của ED nên phương án A là đúng.
• Xét DBCG, theo bất đẳng thức trong tam giác ta có:
BG + CG > BC
Suy ra \(\frac{1}{2}\)BG + \(\frac{1}{2}\)CG > \(\frac{1}{2}\)BC
Mà GD = \(\frac{1}{2}\)BG, GE = \(\frac{1}{2}\)CG (do G là trọng tâm tam giác ABC).
Do đó GD + GE > \(\frac{1}{2}\)BC nên phương án B là sai.
Vậy ta chọn phương án B.
Câu 3:
Cho ∆ABC có AD, BE, CF là ba đường trung tuyến và trọng tâm G.
Cho các phát biểu sau:
(I) \[AD + BE + CF > \frac{3}{4}\left( {AB + BC + AC} \right)\];
(II) AD + BE + CF < AB + BC + AC.
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
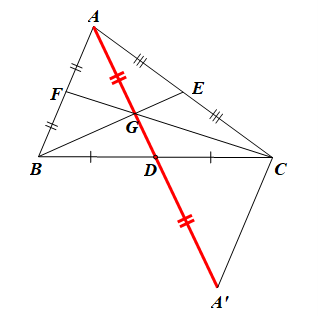
• Ta xét (I):
Vì G là trọng tâm của ∆ABC nên ta có \(GB = \frac{2}{3}BE\) và \(GC = \frac{2}{3}CF\).
∆GBC có GB + GC > BC (bất đẳng thức tam giác).
Suy ra \(\frac{2}{3}BE + \frac{2}{3}CF > BC\).
Hay \(\frac{2}{3}\left( {BE + CF} \right) > BC\).
Do đó \(BE + CF > \frac{3}{2}BC\) (1).
Chứng minh tương tự ta được:
+) \(AD + BE > \frac{3}{2}AB\) (2).
+) \(AD + CF > \frac{3}{2}AC\) (3).
Lấy (1) + (2) + (3) vế theo vế, ta được:
\(2AD + 2BE + 2CF > \frac{3}{2}AB + \frac{3}{2}BC + \frac{3}{2}AC\).
Suy ra \(2\left( {AD + BE + CF} \right) > \frac{3}{2}\left( {AB + BC + AC} \right)\).
Do đó \(AD + BE + CF > \frac{3}{4}\left( {AB + BC + AC} \right)\).
Vậy (I) đúng.
• Ta xét (II):
Trên tia AD, lấy điểm A’ sao cho DA’ = DA.
Xét ∆ADB và ∆A’DC, có:
DA = DA’,
\(\widehat {ADB} = \widehat {A'DC}\) (hai góc đối đỉnh),
BD = CD (do AD là đường trung tuyến của ∆ABC),
Do đó ∆ADB = ∆A’DC (c.g.c).
Suy ra AB = A’C (hai cạnh tương ứng).
Áp dụng bất đẳng thức tam giác cho ∆AA’C, ta được:
AA’ < AC + A’C.
Suy ra AA’ < AC + AB hay 2AD < AC + AB (4).
Chứng minh tương tự, ta được:
+) 2BE < AB + BC (5).
+) 2CF < AC + BC (6).
Lấy (4) + (5) + (6) vế theo vế, ta được:
2AD + 2BE + 2CF < 2AC + 2AB + 2BC.
Suy ra 2(AD + BE + CF) < 2(AB + AC + BC).
Do đó AD + BE + CF < AB + AC + BC.
Vậy (II) đúng.
Kết luận: cả (I) và (II) đều đúng.
Ta chọn phương án C.
