Câu hỏi:
31/01/2024 55
Qua trung điểm H của đoạn thẳng BC, kẻ đường thẳng vuông góc với BC, trên đường thẳng vuông góc đó lấy hai điểm A và I. Nối CA, AB, IB, IC. Phát biểu nào sau đây là đúng nhất:
Qua trung điểm H của đoạn thẳng BC, kẻ đường thẳng vuông góc với BC, trên đường thẳng vuông góc đó lấy hai điểm A và I. Nối CA, AB, IB, IC. Phát biểu nào sau đây là đúng nhất:
A. ABH = ACH;
A. ABH = ACH;
B. IBH = ICH;
C. BAI = CAI;
D. Cả A, B, C đều đúng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
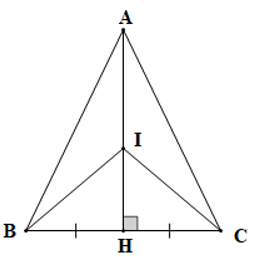
Vì A nằm trên đường thẳng vuông góc với CB tại H nên ta có:
Vì I nằm trên đường thẳng vuông góc với CB tại H nên ta có:
+) Xét ABH và ACH có:
(chứng minh trên),
AH là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ABH = ACH (hai cạnh góc vuông)
Do đó đáp án A đúng
Vì ABH = ACH (chứng minh trên)
Suy ra AB = AC (hai cạnh tương ứng) và (hai góc tương ứng)
+) Xét tam giác HCI và tam giác HBI có:
(chứng minh trên),
HI là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ICH = IBH (hai cạnh góc vuông)
Do đó đáp án B đúng
+) Xét tam giác BAI và tam giác CAI có:
AB = AC (chứng minh trên),
(do ),
AI là cạnh chung
Suy ra BAI = CAI (c.g.c)
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Đáp án đúng là: D
Vì A nằm trên đường thẳng vuông góc với CB tại H nên ta có:
Vì I nằm trên đường thẳng vuông góc với CB tại H nên ta có:
+) Xét ABH và ACH có:
(chứng minh trên),
AH là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ABH = ACH (hai cạnh góc vuông)
Do đó đáp án A đúng
Vì ABH = ACH (chứng minh trên)
Suy ra AB = AC (hai cạnh tương ứng) và (hai góc tương ứng)
+) Xét tam giác HCI và tam giác HBI có:
(chứng minh trên),
HI là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ICH = IBH (hai cạnh góc vuông)
Do đó đáp án B đúng
+) Xét tam giác BAI và tam giác CAI có:
AB = AC (chứng minh trên),
(do ),
AI là cạnh chung
Suy ra BAI = CAI (c.g.c)
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:
Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:
Câu 5:
Cho hình vẽ dưới đây:
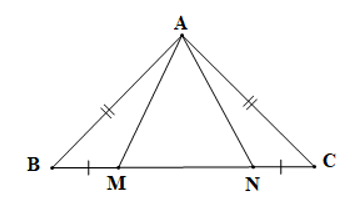
Biết AB = AC, BM = NC, . Xét các khẳng định sau:
(1) ABM = ACN;
(2) ABN = ACM.
Chọn câu đúng:
Cho hình vẽ dưới đây:
Biết AB = AC, BM = NC, . Xét các khẳng định sau:
(1) ABM = ACN;
(2) ABN = ACM.
Chọn câu đúng:
Câu 6:
Cho tam giác HIK và tam giác DEG có IH = DE, HK = EG. Phát biểu nào sau đây là đúng:
Cho tam giác HIK và tam giác DEG có IH = DE, HK = EG. Phát biểu nào sau đây là đúng:
Câu 7:
Cho tam giác ABC có AB = AC = BC, phân giác BH và CK cắt nhau tại I. Cho các phát biểu sau:
(I) CK AB;
(II) BH CK ;
(III) BH AC;
(IV)
Số phát biểu đúng là:
Cho tam giác ABC có AB = AC = BC, phân giác BH và CK cắt nhau tại I. Cho các phát biểu sau:
(I) CK AB;
(II) BH CK ;
(III) BH AC;
(IV)
Số phát biểu đúng là:
Câu 8:
Cho tam giác MNP và tam giác DEF có: MN = DE, Điều kiện để DEF = NMP theo trường hợp cạnh – góc – cạnh là:
Cho tam giác MNP và tam giác DEF có: MN = DE, Điều kiện để DEF = NMP theo trường hợp cạnh – góc – cạnh là:
Câu 9:
Cho hình vẽ dưới đây:
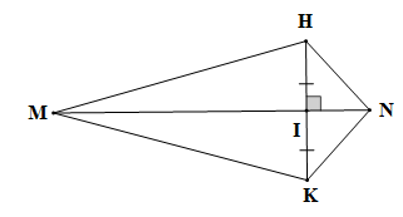
Số cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh là:
Cho hình vẽ dưới đây:
Số cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh là:
Câu 10:
Cho hình vẽ sau:
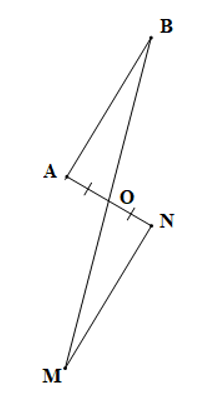
Điều kiện để ABO = NMO theo trường hợp cạnh – góc – cạnh là:
Cho hình vẽ sau:
Điều kiện để ABO = NMO theo trường hợp cạnh – góc – cạnh là:
Câu 12:
Cho góc xOy tù , gọi Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm M, trên tia Oy lấy điểm N sao cho OM = ON. Trên tia đối của tia Oz lấy điểm I tuỳ ý. Chọn phát biểu đúng nhất:
Cho góc xOy tù , gọi Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm M, trên tia Oy lấy điểm N sao cho OM = ON. Trên tia đối của tia Oz lấy điểm I tuỳ ý. Chọn phát biểu đúng nhất:
Câu 14:
Cho DABC = DMNP. D, E, Q, R lần lượt là trung điểm của BC, CA, NP, PM. Khẳng định nào sau đây là sai?
Cho DABC = DMNP. D, E, Q, R lần lượt là trung điểm của BC, CA, NP, PM. Khẳng định nào sau đây là sai?


