Gọi chiều dài, chiều rộng và chiều cao của bể cá lần lượt là a, b, c (a, b, c > 0).
Theo đề bài ta có a = 2b
Vì ông A dự định sử dụng hết 5m2 kính để làm bể cá không nắp nên diện tích toàn phần (bỏ 1 mặt đáy) của hình hộp là: ab + 2bc + 2ac
Hay ab + 2bc + 2ac = 5.
Mà a = 2b nên 2b2 + 2bc + 4bc = 5
Û 2b2 + 6bc = 5
\( \Rightarrow c = \frac{{5 - 2{b^2}}}{{6b}}\).
Xét điều kiện c > 0 \( \Rightarrow \frac{{5 - 2{b^2}}}{{6b}} > 0 \Rightarrow 5 - 2{b^2} > 0\)
\( \Rightarrow 0 < b < \sqrt {\frac{5}{2}} \).
Thể tích bể cá là:
\(V = abc = 2b\,.\,b\,.\,\frac{{5 - 2{b^2}}}{{6b}} = \frac{{ - 2{b^3} + 5b}}{3}\).
Xét hàm số \(f\left( b \right) = \frac{{ - 2{b^3} + 5b}}{3}\;\left( {b > 0} \right)\)
\( \Rightarrow f'\left( b \right) = \frac{{ - 6{b^2} + 5}}{3} = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}b = - \sqrt {\frac{5}{6}} \;\left( {KTM} \right)\\b = \sqrt {\frac{5}{6}} \;\;\;\left( {TM} \right)\end{array} \right.\)
Xét bảng biến thiên:
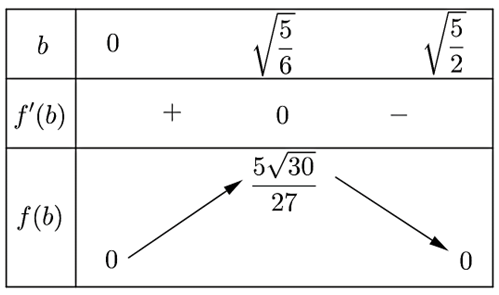
Yêu cầu bài toán suy ra \(\max f\left( b \right) = \frac{{5\sqrt {30} }}{{27}} \Leftrightarrow b = \sqrt {\frac{5}{6}} \).
Vậy bể cá có thể tích lớn nhất bằng \[\frac{{5\sqrt {30} }}{{27}} \approx 1,01\;\left( {{m^3}} \right)\].